题目内容
某同学在“用单摆测定重力加速度”的实验中，测量5种不同摆长情况下单摆的振动周期，记录表格如下：| L（m） | 0.5 | 0.8 | 0.9 | 1.0 | 1.2 |
| T（s） | 1.42 | 1.79 | 1.90 | 2.00 | 2.20 |
| T2（s2） | 2.02 | 3.20 | 3.61 | 4.00 | 4.84 |
②该同学在实验中测算出的g值比当地的公认值偏大，其原因可能是
A．振幅偏小
B．摆球质量偏大
C．将振动次数n记为（n+1）
D．将摆线长当作摆长，未加摆球的半径．
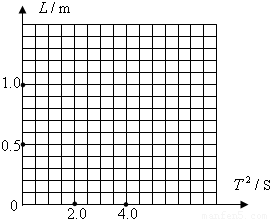
【答案】分析：（1）根据表格中数据，采用描点法，作出图象，根据单摆的周期公式T=2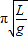
，得到T2与L的表达式，由图象读取斜率，求得g；
（2）根据单摆的周期公式T=2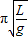
，分析误差的原因．
解答：解：（1）作出L-T2图线如图所示，由单摆的周期公式T=2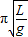
，得L=
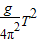
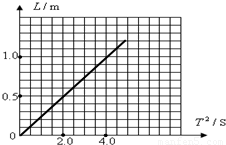
根据数学知识得知：L-T2图线的斜率k=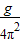
由图得到，k=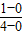
=0.25
联立解得，g=9.86m/s2
（2）由T=2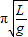
，得g=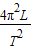
A、B单摆的周期与振幅、摆球的质量无关，故AB均错误．
C、将振动次数n记为（n+1），测得的单摆周期T偏小，则知g的测量偏大．故C正确．
D、将摆线长当作摆长，未加摆球的半径，摆长偏小，则知g的测量偏小．故D错误．
故选C
故答案为：
①9.86m/s2
②C
点评：本题考查单摆实验方法和数据处理的能力．对于实验误差，关键从实验原理出发进行分析．
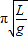，得到T2与L的表达式，由图象读取斜率，求得g；（2）根据单摆的周期公式T=2
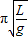，分析误差的原因．解答：解：（1）作出L-T2图线如图所示，由单摆的周期公式T=2
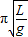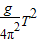
，得L=根据数学知识得知：L-T2图线的斜率k=
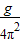
由图得到，k=
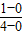=0.25联立解得，g=9.86m/s2
（2）由T=2
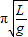，得g=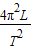A、B单摆的周期与振幅、摆球的质量无关，故AB均错误．
C、将振动次数n记为（n+1），测得的单摆周期T偏小，则知g的测量偏大．故C正确．
D、将摆线长当作摆长，未加摆球的半径，摆长偏小，则知g的测量偏小．故D错误．
故选C
故答案为：
①9.86m/s2
②C
点评：本题考查单摆实验方法和数据处理的能力．对于实验误差，关键从实验原理出发进行分析．
练习册系列答案
相关题目
某实验小组在进行“用单摆测定重力加速度”的实验中，已知单摆在摆动过程中的摆角小于5°；在测量单摆的周期时，从单摆运动到最低点开始计时且记数为1，到第n次经过最低点所用的时间内为t；在测量单摆的摆长时，先用毫米刻度尺测得悬挂后的摆线长（从悬点到摆球的最上端）为L，再用游标卡尺测得摆球的直径为d．
某同学在做“用单摆测定重力加速度”的实验．
某同学在做用单摆测定重力加速度的实验中，用游标为50分度的卡尺测量小球的直径，结果如图所示．由图可知小球的直径为