Question

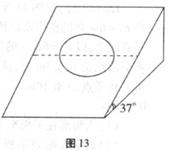
如图13所示，有一倾角为θ的斜面，其底端固定一挡板M，另有三个木块A、B和C，它们的质量分别为m_A=m_B=m，m_C=3m，它们与斜面间的动摩擦因数都相同.其中木块A放于斜面上并通过一轻弹簧与挡板M相连.开始时，木块A静止在P处，弹簧处于自然伸长状态.木块B在Q点以初速度v₀向下运动，P、Q间的距离为L.已知木块B在下滑过程中做匀速直线运动，与木块A相撞后立刻一起向下运动，但不粘连.它们到达一个最低点后又向上运动，木块B向上运动恰好能回到Q点.若木块A仍静放于P点，木块C从Q点处开始以初速度v₀向下运动，经历同样过程，最后木块C停在斜面的R点，求A、R间的距离L′的大小.

图13

Answer 1

木块B下滑做匀速直线运动，有mgsinθ=μmgcosθ

即gsinθ=μgcosθ①

B和A相撞前后，总动量守恒，mv₀=2mv₁

∴v₁=v₀/2    ②

设两木块向下压缩弹簧的最大长度为s，两木块被弹簧弹回到P点时的速度为v₂，则

μ2mgcosθ·2s=mv₁²-·    ③

两木块在P点处分开后，木块B上滑到Q点的过程：

(mgsinθ+μmcosθ)L=    ④

木块C与A碰撞前后总动量守恒，

3m·v₀=4m·v′₁

∴v′₁=v₀    ⑤

设木块C和A压缩弹簧的最大长度为s′，两木块被弹簧回到P点时的速度为v′₂，则

μ4mgcosθ·2s′=·-·    ⑥

木块C与A在P点处分开后，木块C上滑到R点的过程：

(3mgsinθ+μ3mgcosθ)L′=·      ⑦

由式①可知在木块压缩弹簧的过程中，重力对木块所做的功与摩擦力对木块所做的功大小相等，因此弹簧被压缩而具有的最大弹性势能等于开始压缩时两木块的总动能.

∵木块B和A压弹簧的初动能E_k1=·mv₁²=

木块C和A压缩弹簧的初动能E_k2=·4mv′₁²=

即E_k1=E_k2，因此弹簧前后两次的最大压缩量相等，即s=s′    ⑧

联立式①至式⑧，解得L′=L-.