题目内容
如图所示，一带电粒子（重力不计）在匀强磁场中沿图中所示轨迹运动，中央是一块薄绝缘板，粒子在穿过绝缘板时有动能损失，由图可知（ ）分析：由牛顿第二定律及向心力公式可知粒子转动半径与速度的关系，则可判断粒子在穿过绝缘板前后的运动情况； 由周期公式可知上下两部分的时间关系．
解答：解：由Bqv=m
可知，r=
； 因粒子在穿过板后速度减小，则粒子的半径减小，故说明粒子是由下向上穿过，故运动方向为edcba； 故A错误，B正确；
粒子受力指向圆心，则由左手定则可知粒子应带正电，故C错误；
因粒子转动的周期T=
，在转动中磁场强度及质量没有变化，故周期不变，而由图可知，粒子在上下都经过半个周期，故时间相等； 故D错误；
故选B．
| v2 |
| r |
| mv |
| Bq |
粒子受力指向圆心，则由左手定则可知粒子应带正电，故C错误；
因粒子转动的周期T=
| 2πm |
| Bq |
故选B．
点评：带电粒子在磁场中运动的考查的重点为牛顿第二定律及向心力公式的应用，不过在选择题中可以直接应用结论r=
及T=
．
| mv |
| Bq |
| 2πm |
| Bq |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，一带电粒子在两个固定的等量正点电荷的电场中运动，图中的实线为等势面，虚线ABC为粒子的运动轨迹，其中B点是两点电荷连线的中点，A、C位于同一等势面上．下列说法正确的是（ ）
（2005?长宁区模拟）如图所示，一带电粒子以速度v0沿上板边缘垂直于电场线射入匀强电场，它刚好贴着下板边缘飞出．已知匀强电场两极板长为l，间距为d，求：
如图所示，一带电粒子以某速度进入水平向右的匀强电场中，在电场力作用下形成图中所示的运动轨迹．M和N是轨迹上的两点，其中M点在轨迹的最右点．不计重力，下列表述正确的是（ ）
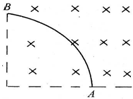如图所示，一带电粒子垂直射入一自左向右逐渐增强的磁场中，由于周围气体的阻尼作用，其运动径迹的为一段圆弧线，则从图中可以判断（不计重力）（ ）| A、粒子从A点射入，速率逐渐减小 | B、粒子从A点射入，速率逐渐增大 | C、粒子带负电，从B点射入磁场 | D、粒子带正电，从A点射入磁场 |
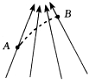如图所示，一带电粒子只受电场力从A飞到B，径迹如图中虚线所示，下列说法正确的是（ ）| A、粒子带正电 | B、粒子加速度不断变小 | C、粒子在A点时动能较大 | D、B点场强小于A点场强 |