题目内容
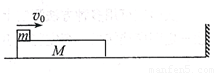
如图所示，一足够长木板，质量为M，放在光滑水平面上，在其左端放一质量为m的小木块（可视为质点），m>M，木块与木板间存在摩擦，现使两者以速度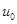
共同向右运动。已知木板与墙碰撞后立即反向且速度大小不变，木块不会滑离木板和碰到墙。求木板在第二次碰墙后的运动过程中，木板速度为零时木块的速度。
【答案】
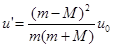
【解析】第一次碰墙后，木板原速率反向瞬间，木块速度不变，木板与木块最终一起以共同速度向右运动，
由运量实恒定律得（m-M)u0=（m+M)u （2分）
得u=（m-M）u0/（m+M) （1分）
第二次碰墙后，当木板速度为零时，由动量守恒定律得（m-M) u=mu’（1分）
得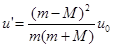 （1分）
练习册系列答案
相关题目
（2013?德州二模）如图所示，AB段为一半径R=0.2m的光滑
（2011?湖南模拟）如图所示，足够长的水平传送带始终以v=3m/s的速度大小向左运动，传送带上有一质量为M=2kg、左侧面开口的小木盒A，A与传送带之间的动摩擦因数为μ=0.3，开始时，A与传送带之间保持相对静止．先后相隔△t=3s有两个质量m=1kg的光滑小球B自传送带的左端出发，以v0=15m/s的速度大小在传送带上向右运动．第1个球与木盒相遇后立即进入盒中且与盒粘合在一起获得方向向右的共同速度，这个相遇粘合的过程时间极短，损失的机械能△E=108J；第2个球出发后历时△t=
如图所示，质量M=20kg的木楔ABC静置于粗糙水平地面上，在木楔倾角θ=30°足够长的斜面上，有一质量m=4.0kg的物块由静止开始沿斜面下滑．当物块滑行的距离x=2.5m时，它的速度v=5m/s，在这一过程中木楔没有动，重力加速度取g=10m/s2．求：