题目内容
如图,在竖直面内的坐标系xoy中,x轴上方存在竖直向下的匀强电场,电场强度 E =12N/C,在x轴下方存在垂直纸面向里的的匀强磁场,磁感应强度B =2T,一带电量为q = +3×10-4c、质量为m=3.6×10-4kg的小球,从(1m ,0.5m)处以初速度v0沿x轴负方向抛出,刚好经坐标原点与x轴成45°,沿切线方向进入图中半径为R1
=  m的光滑圆弧轨道Ⅰ,再次经
x轴沿切线方向进入半径为R2=
m的光滑圆弧轨道Ⅰ,再次经
x轴沿切线方向进入半径为R2= m,的光滑圆弧轨道Ⅱ,求:(g取10m/s2)
m,的光滑圆弧轨道Ⅱ,求:(g取10m/s2)
⑴小球抛出时的初速度;
⑵小球到达轨道Ⅰ的最低点时对轨道的压力;
⑶若小球从从第一象限某位置沿x轴负向抛出后 均能通过坐标原点沿切线方向进入轨道Ⅰ,再沿轨道Ⅱ外侧到达最高点,求小球抛出的所有可能位置。

⑴由题意知:Eq=mg=3.6×N,则: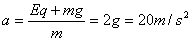
由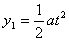 得 t=
得 t=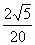 s
由x1 = v0 t 得
s
由x1 = v0 t 得
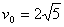 m/s
m/s
⑵设小球到达轨道Ⅰ最底点的速度为v1,所受支持力为FN,洛化兹力为FB,则:
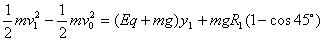 代入数据得:v1 = 8m/s
代入数据得:v1 = 8m/s
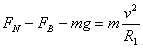 代入数据得FN=4.56×N
代入数据得FN=4.56×N
即此时小球对轨道Ⅰ的压力为4.56×N
⑶因小球达坐标原点时的速度偏向角为45°,则小球的位移偏向角正切值为0.5,即小球抛出点的位置必在方程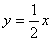 上。
上。
(Ⅰ)设小球从(x2,y2)处以初速度v01抛出,达轨道Ⅱ最高点的速度为零,则:
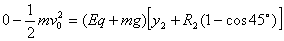
代入数据并化简得: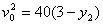
由: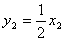
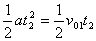 得:20t2 = v01
得:20t2 = v01
由上两式得: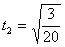 s
s
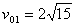 (m/s)
(m/s)
故: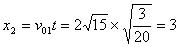 (m)
(m)
(Ⅱ)设小球从(x3,y3)处以初速度v02抛出,达轨道Ⅱ最高点的最大速度为v2,则:

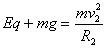 代入数据并化简得:
代入数据并化简得: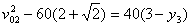
得: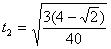 s
s 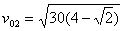 m/s
m/s
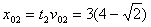 m
m
由此可知:要让小球到达轨道Ⅱ的最高点,小球抛出的位置在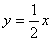 上,
上,
区间为3m≤x≤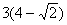 m
m

 如图甲所示,一竖直面内的轨道是由粗糙斜面AB和光滑圆轨道BCD组成,AB与BCD相切于B点,C为圆轨道的最低点.将小物块(可看作质点)置于轨道ABC上离地面高为H处由静止下滑,可用力传感器测出其经过C点时对轨道的压力FN.现将小物块放在ABC上不同高度处,让H从零开始逐渐增大,传感器测出小物块每次从不同高度处下滑到C点时对轨道的压力FN,得到如图乙两段直线PQ和QI,且IQ反向延长线与纵轴交点坐标值为5N,g取10m/s2.则
如图甲所示,一竖直面内的轨道是由粗糙斜面AB和光滑圆轨道BCD组成,AB与BCD相切于B点,C为圆轨道的最低点.将小物块(可看作质点)置于轨道ABC上离地面高为H处由静止下滑,可用力传感器测出其经过C点时对轨道的压力FN.现将小物块放在ABC上不同高度处,让H从零开始逐渐增大,传感器测出小物块每次从不同高度处下滑到C点时对轨道的压力FN,得到如图乙两段直线PQ和QI,且IQ反向延长线与纵轴交点坐标值为5N,g取10m/s2.则

 =60°。请你再结合图象所给的信息求出斜面对小物体的滑动摩擦力大小为多少?
=60°。请你再结合图象所给的信息求出斜面对小物体的滑动摩擦力大小为多少?