Question

质量为800kg的小汽车驶过一半径为50m的圆形拱桥，到桥顶时的速度为5m/s，g=10m/s²，求：
（1）此时汽车对桥的压力．
（2）若汽车到达桥顶时对桥的压力为零，且车不脱离桥面，到达桥顶时汽车的速度是多大？

Answer 1

分析：（1）在最高点重力和支持力的合力提供向心力，根据向心力公式和牛顿第二定律可列式求解；
（2）汽车对桥恰好无压力，重力完全提供向心力，根据向心力公式和牛顿第二定律可列式求解．

解答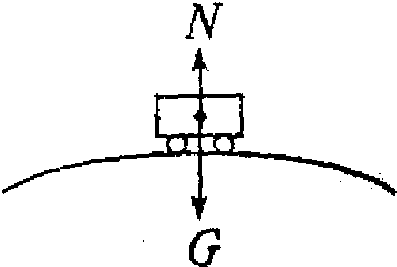：解：（1）如图所示，汽车到达桥顶时，竖直方向受到重力G和桥对它的支持力N的作用．汽车对桥顶的压力大小等于桥顶对汽车的支持力N，汽车过桥时做圆周运动，重力和支持力的合力提供向心力，即：F=G-N；
根据向心力公式：F=m

v2

r

有：N=G-F=mg-m

v2

r

=7600N，
根据牛顿第三定律可知
此时汽车对桥的压力为7600N，方向竖直向下
（2）汽车经过桥顶恰好对桥没有压力，则N=0，即汽车做圆周运动的向心力完全由其自身重力来提供，所以有：
F=G=m

v2

r

解得：v=10

5

m/s
答：（1）此时汽车对桥的压力为7600N，方向竖直向下；
（2）到达桥顶时汽车的速度是10

5

m/s

点评：本题关键找出车经过桥的最高点时的向心力来源，然后根据牛顿第二定律和向心力公式列式求解！