题目内容
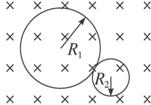
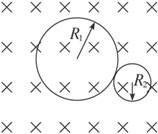
静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44∶1,如图所示,则( )
A.α粒子与反冲核的动量大小相等,方向相反
B.原来放射性元素的原子核电荷数为90
C.反冲核的核电荷数为88
D.α粒子和反冲核的速度之比为1∶88
【答案】
ABC
【解析】
试题分析:粒子之间相互作用的过程中遵守动量守恒,由于初始总动量为零,则末动量也为零,即α粒子和反冲核的动量大小相等,方向相反.
由于释放的α粒子和反冲核均在垂直于磁场的平面内且在洛伦兹力作用下做圆周运动.
由Bqv=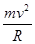 得R=
得R=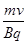 ,
,
若原来放射性元素的核电荷数为Z,
则对于α粒子有R1=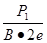 对反冲核
对反冲核
R2=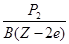 由于P1=P2,得R1∶R2=44∶1,
由于P1=P2,得R1∶R2=44∶1,
得Z=90.
它们的速度大小与质量成反比,D项错误,上述选项正确的为A、B、C
考点:洛伦兹力 匀速圆周运动 动量守恒
点评:放射性物质在释放新核时会产生类似反冲问题,而动量守恒的典型模型就是碰撞、爆炸、反冲。所以在这部分问题时核子内部的作用力会远大于外力,会结合到动量守恒定律的问题。

练习册系列答案
相关题目
 静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则( )
静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则( )