题目内容
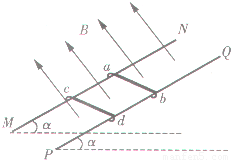
如图所示,两足够长平行光滑的金属导轨MN、PQ相距为L,导轨平面与水平面夹角α=30°,导轨电阻不计.磁感应强度为B的匀强磁场垂直导轨平面向上,两根长为乙的完全相同的金属棒ab、cd垂直于MN、PQ放置在导轨上,且与导轨电接触良好,每根棒的质量为m、电阻为R.现对ab施加平行导轨向上的恒力F,当ab沿导轨向上做匀速直线运动时,cd保持静止状态.(1)求力F的大小及ab运动的速度大小;
(2)若施加在ab上力的大小变为2mg,方向不变,经过一段时间后ab、cd以相同加速度沿导轨向上加速运动,求此时ab棒与cd棒的速度差(△v=vab-vcd).
【答案】分析:(1)由题,ab沿导轨向上做匀速直线运动时,cd保持静止状态,两棒都处于平衡状态,合力都为零,分析两棒的受力情况,根据平衡条件,分别对两棒列式,即可求解F的大小.由法拉第定律、欧姆定律推导出安培力与速度的关系式,由平衡条件可求出ab运动的速度.
(2)当两以相同的加速度沿导轨向上加速运动时,回路中感应电动势E=BL(vab-vcd)=BL△v.先根据牛顿第二定律分别对整体和cd棒列式,求出感应电流I,再根据欧姆定律E=I?2R,结合法拉第定律可求出速度差.
解答:解:(1)由题知,两棒都处于平衡状态,两棒所受的合外力均为零,则根据平衡条件得:
对ab棒:F-Fab-mgsinα=0
对cd棒:Fcd-mgsinα=0
ab、cd两棒所受的安培力大小为:Fab=Fcd=BIL=B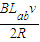 L=
L=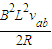
由以上三式得:F=2mgsinα,vab=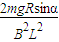 =
=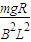
(2)当ab、cd以相同的加速度a运动时,根据牛顿第二定律得:
对整体:2mg-2mgsinα=2ma
对cd棒:BIL-mgsinα=ma
联立以上两式得 I=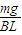
由闭合电路欧姆定律得:感应电动势为 E=I?2R=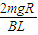
又根据法拉第电磁感应定律得:感应电动势E=BL(vab-vcd)=BL△v.
解得△v=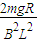
答:
(1)力F的大小为2mgsinα,ab运动的速度大小为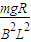 .
.
(2)此时ab棒与cd棒的速度差为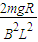 .
.
点评:本题是电磁感应中的力学问题,综合运用电磁学知识、力平衡知识和牛顿第二定律进行求解.
(2)当两以相同的加速度沿导轨向上加速运动时,回路中感应电动势E=BL(vab-vcd)=BL△v.先根据牛顿第二定律分别对整体和cd棒列式,求出感应电流I,再根据欧姆定律E=I?2R,结合法拉第定律可求出速度差.
解答:解:(1)由题知,两棒都处于平衡状态,两棒所受的合外力均为零,则根据平衡条件得:
对ab棒:F-Fab-mgsinα=0
对cd棒:Fcd-mgsinα=0
ab、cd两棒所受的安培力大小为:Fab=Fcd=BIL=B
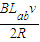 L=
L=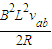
由以上三式得:F=2mgsinα,vab=
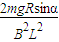 =
=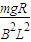
(2)当ab、cd以相同的加速度a运动时,根据牛顿第二定律得:
对整体:2mg-2mgsinα=2ma
对cd棒:BIL-mgsinα=ma
联立以上两式得 I=
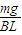
由闭合电路欧姆定律得:感应电动势为 E=I?2R=
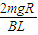
又根据法拉第电磁感应定律得:感应电动势E=BL(vab-vcd)=BL△v.
解得△v=
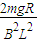
答:
(1)力F的大小为2mgsinα,ab运动的速度大小为
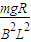 .
.(2)此时ab棒与cd棒的速度差为
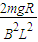 .
.点评:本题是电磁感应中的力学问题,综合运用电磁学知识、力平衡知识和牛顿第二定律进行求解.

练习册系列答案
相关题目
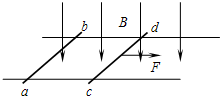 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
 如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )
如图所示,两足够长平行金属导轨固定在水平面上,匀强磁场方向垂直导轨平面向下,金属棒ab、cd与导轨构成闭合回路且都可沿导轨无摩擦滑动,两金属棒ab、cd的质量之比为2:1,用一沿导轨方向的恒力F水平向右拉金属棒cd,经过足够长时间以后( )