题目内容
如图所示,直角坐标系xOy,X轴正方向沿着绝缘粗糙水平面向右,y轴正方向竖直向上.空间充满沿X轴负方向、E=2.0×104N/C的匀强电场.一个质量m=2.0×10-3kg、电量q=2.0×10-6C的带正电的物块(可作为质点),从O点开始以v=10.0m/s的初速度沿着X轴正方向做直线运动,物块与水平面间动摩擦因数μ=0.5,g=10m/s2.(1)求带电物体在t=0.8s内通过的位移x
(2)若在0.8s末突然将匀强电场的方向变为沿y轴正方向,场强大小保持不变.求在0?1.0s内带电物体电势能的变化量△E.

【答案】分析:(1)带电物体在t=0.8s内,水平方向受到向左的滑动摩擦力和电场力,先向右做匀减速运动,根据牛顿第二定律得到加速度a1,由运动学公式求出匀减速到停下的时间和位移.之后物体向左做匀加速运动,由牛顿第二定律和运动学公式结合求出时间和位移,即可求出物体在t=0.8s内通过的位移x.
(2)0.8s内电场力做功为W1=-Eqx.0.8s后,带电物块受到竖直向上的电场力F=Eq=4.0×10-2N>mg,带电物块开始在水平方向做匀速运动,竖直方向做初速为零的匀加速运动,由牛顿第二定律和运动学公式结合求出竖直方向的位移y,电场力对带电物块做功为W2=Eqy,则0~1.0s内电场力对带电物块所做的总功为W=W1+W2.
解答:解:(1)设带电物块向右做匀减速直线运动过程中,加速度大小为a1,时间为t1,通过的位移为x1,则
Eq+μmg=ma1,
又t1=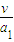 ,x1=
,x1=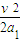
代入解得a1=25 m/s2,t1=0.4 s,x1=2 m
t1=0.4s之后,带电物块向左做匀加速直线运动,设加速度大小为a2,时间为t2,通过的位移为x2,则
Eq-μmg=ma2 得a2=15m/s2,
由题,t2=t-t1=0.4s
x2= a2t22=1.2m
a2t22=1.2m
所以x=x1-x2=0.8m,方向水平向右.
(2)设0.8s内电场力做功为W1,则
W1=-Eqx=-3.2×10-2J
0.8s后,设带电物块受到竖直向上的电场力为F,且F=Eq=4.0×10-2N>mg,所以,带电物块开始在水平方向做的匀速运动,竖直方向做初速为零的匀加速运动,设加速度为a3,在竖直方向的位移为y,电场力做功为W2,则
F-mg=ma3
解得a3=10m/s2,
又 t3=1.0-t1=0.2s
则得 y= a3t32=0.2m
a3t32=0.2m
电场力做功 W2=Eqy=8.0×10-3J
设0~1.0s内电场力对带电物块所做的总功为W,则
W=W1+W2=-2.4×10-2J
即△E=-W=2.4×10-2J
答:
(1)求带电物体在t=0.8s内通过的位移x是0.8m,方向水平向右.
(2)在0?1.0s内带电物体电势能的变化量△E是2.4×10-2J.
点评:本题的解题关键是根据牛顿第二定律和运动学分析物体的运动情况,通过定量计算分析运动过程.
(2)0.8s内电场力做功为W1=-Eqx.0.8s后,带电物块受到竖直向上的电场力F=Eq=4.0×10-2N>mg,带电物块开始在水平方向做匀速运动,竖直方向做初速为零的匀加速运动,由牛顿第二定律和运动学公式结合求出竖直方向的位移y,电场力对带电物块做功为W2=Eqy,则0~1.0s内电场力对带电物块所做的总功为W=W1+W2.
解答:解:(1)设带电物块向右做匀减速直线运动过程中,加速度大小为a1,时间为t1,通过的位移为x1,则
Eq+μmg=ma1,
又t1=
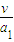 ,x1=
,x1=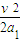
代入解得a1=25 m/s2,t1=0.4 s,x1=2 m
t1=0.4s之后,带电物块向左做匀加速直线运动,设加速度大小为a2,时间为t2,通过的位移为x2,则
Eq-μmg=ma2 得a2=15m/s2,
由题,t2=t-t1=0.4s
x2=
 a2t22=1.2m
a2t22=1.2m 所以x=x1-x2=0.8m,方向水平向右.
(2)设0.8s内电场力做功为W1,则
W1=-Eqx=-3.2×10-2J
0.8s后,设带电物块受到竖直向上的电场力为F,且F=Eq=4.0×10-2N>mg,所以,带电物块开始在水平方向做的匀速运动,竖直方向做初速为零的匀加速运动,设加速度为a3,在竖直方向的位移为y,电场力做功为W2,则
F-mg=ma3
解得a3=10m/s2,
又 t3=1.0-t1=0.2s
则得 y=
 a3t32=0.2m
a3t32=0.2m电场力做功 W2=Eqy=8.0×10-3J
设0~1.0s内电场力对带电物块所做的总功为W,则
W=W1+W2=-2.4×10-2J
即△E=-W=2.4×10-2J
答:
(1)求带电物体在t=0.8s内通过的位移x是0.8m,方向水平向右.
(2)在0?1.0s内带电物体电势能的变化量△E是2.4×10-2J.
点评:本题的解题关键是根据牛顿第二定律和运动学分析物体的运动情况,通过定量计算分析运动过程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2009?宁夏)空间有一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点的坐标为(a,
(2009?宁夏)空间有一均匀强电场,在电场中建立如图所示的直角坐标系O-xyz,M、N、P为电场中的三个点,M点的坐标(0,a,0),N点的坐标为(a,0,0),P点的坐标为(a, 在如图所示的直角坐标系xyz所在的区域内,存在电场强度为E的匀强电场和磁感强度为B的匀强磁场.已知从坐标原点O沿x轴的正方向射入质子,穿过这区域时未发生偏转.设重力可忽略不计,则这区域中的E和B的方向可能是( )
在如图所示的直角坐标系xyz所在的区域内,存在电场强度为E的匀强电场和磁感强度为B的匀强磁场.已知从坐标原点O沿x轴的正方向射入质子,穿过这区域时未发生偏转.设重力可忽略不计,则这区域中的E和B的方向可能是( ) 如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求:
如图所示,直角坐标系的ox轴水平,oy轴竖直;M点坐标为(-0.3m,0)、N点坐标为(-0.2m,0);在-0.3m≤X≤-0.2m的长条形范围内存在竖直方向的匀强电场E0;在X≥0的范围内存在竖直向上的匀强电场,场强为E=20N/C;在第一象限的某处有一圆形的匀强磁场区,磁场方向垂直纸面向外,磁感应强度B=2.5T.有一带电量q=+1.0×10-4C、质量m=2×10-4kg的微粒以v0=0.5m/s的速度从M点沿着x轴正方向飞入电场,恰好垂直经过y轴上的P点(图中未画出,yP>0),而后微粒经过第一象限某处的圆形磁场区,击中x轴上的Q点,速度方向与x轴正方向夹角为60°.g取10m/s2.求: 如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴正方向夹角为θ.不计空气阻力,重力加速度为g,求:
如图所示,直角坐标系xOy位于竖直平面内,在水平的x轴下方存在匀强磁场和匀强电场,磁场的磁感应强度为B,方向垂直xOy平面向里,电场线平行于y轴.一质量为m、电荷量为q的带正电的小球,从y轴上的A点水平向右抛出,经x轴上的M点进入电场和磁场,恰能做匀速圆周运动,从x轴上的N点第一次离开电场和磁场,MN之间的距离为L,小球过M点时的速度方向与x轴正方向夹角为θ.不计空气阻力,重力加速度为g,求: 在如图所示的直角坐标系中,第一象限内存在着一个水平宽度为L
在如图所示的直角坐标系中,第一象限内存在着一个水平宽度为L