题目内容
如图所示，在同一均匀介质中有S1、S2两个波源，这两个波源的频率、振动方向均相同，且振动的步调完全一致，S1、S2之间相距两个波长，B点为S1、S2连线的中点；今以B点为圆心，以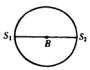
为半径画圆，问在该圆周上(S1、S2两波源除外)共有几个振动加强的点?
答案：
解析：
提示：
解析：
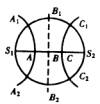
| 首先让我们分析S1、S2两波源的连线上共有几个振动加强的点.由对称性可直接判断B点为加强点，设A点为BS1中点，C点为S2中点，又AS2-AS1=λ，CS1-CS2=λ，故A、C两点也为加强点(见图)，即S1，S2连线上共有三个加强点，再过.A、B、C三点作三条加强线(表示三个加强区域)交圆周上A1、A2，B1、B2、C1、C2六点.显然这六个点也为加强点，故圆周上共有六个加强点.
|
提示：
| 波的干涉
|
练习册系列答案
相关题目
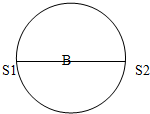如图所示，在同一均匀介质中有S1，S2两个波源，这两个波源的频率、振动步调均相同，S1、S2之间相距两个波长，B点S1、S2为连线的中点，今以B点为圆心，以BS1为半径画圆，则在圆周上（S1、S2两波源除外）共有
如图所示，在同一均匀介质中有S1和S2两个振动情况完全相同的波源，现将S1S2连线分成四等份，若每一等份恰好等于半个波长，则图中各等分点处质点P、Q、R的运动情况为（ ）| A、Q质点总处于波谷 | B、P、R两质点总处于波峰 | C、Q质点总处于静止 | D、P、Q、R质点振动总是加强 |
如图所示，在同一均匀介质中有S1和S2两个振动情况完全相同的波源，现将S1S2连线分成四等份，若每一等份恰好等于半个波长，则图中各等分点处质点P、Q、R的运动情况为
| A．Q质点总处于波谷 | B．P、R两质点总处于波峰 |
| C．Q质点总处于静止 | D．P、Q、R质点振动总是加强 |
