题目内容
质量为m1、m2的两个星球组成双星，它们在相互之间的万有引力作用下绕两球连线上某点O做匀速圆周运动，则它们各自运动的周期T1：T2= ，半径r1：r2= ，线速度v1：v2= ，向心加速度a1：a2= ．
【答案】分析：双星靠相互间的万有引力提供向心力，周期相等．根据
，
，求出轨道半径比．周期相同，则ω相同，根据v=rω求出线速度之比．根据a=rω2，求出向心加速度之比．
解答：解：双星靠相互间的万有引力提供向心力，周期相等，角速度相等．所以周期比T1：T2=1：1．
根据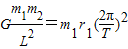
，
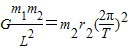，知m1r1=m2r2，则半径r1：r2=m2：m1．
根据v=rω得，
v1：v2=r1：r2=m2：m1．
根据a=rω2得，a1：a2=r1：r2=m2：m1．
故本题答案为：1：1，m2：m1，m2：m1，m2：m1．
点评：解决本题的关键知道双星靠相互间的万有引力提供向心力，周期相等，角速度相等．根据m1r1=m2r2，得出轨道半径比，以及根据v=rω，a=rω2，得出线速度之比、向心加速度之比．
，，求出轨道半径比．周期相同，则ω相同，根据v=rω求出线速度之比．根据a=rω2，求出向心加速度之比．解答：解：双星靠相互间的万有引力提供向心力，周期相等，角速度相等．所以周期比T1：T2=1：1．
根据
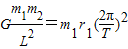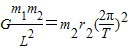，，知m1r1=m2r2，则半径r1：r2=m2：m1．根据v=rω得，
v1：v2=r1：r2=m2：m1．
根据a=rω2得，a1：a2=r1：r2=m2：m1．
故本题答案为：1：1，m2：m1，m2：m1，m2：m1．
点评：解决本题的关键知道双星靠相互间的万有引力提供向心力，周期相等，角速度相等．根据m1r1=m2r2，得出轨道半径比，以及根据v=rω，a=rω2，得出线速度之比、向心加速度之比．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
如图所示，一轻绳跨过定滑轮悬挂质量为m1、m2的两个物体，滑轮质量和所有摩擦均不计，m1＜m2，系统由静止开始运动的过程中（m1未跨过滑轮）（ ）
如图所示，轻绳两端分别系有质量为m1和m2的两个小球，m1沿半球形光滑碗面下滑到P点处于平衡，O为球心，C处光滑，∠COP等于60，碗对m1的支持力为FN，绳对m2的拉力为FT，则下列各式中正确的是（ ）
（2013?徐汇区一模）如图所示，圆心在O点、半径为R的光滑圆弧轨道ABC竖直固定在水平桌面上，OC与OA的夹角为60°，轨道最低点A与桌面相切．一足够长的轻绳两端分别系着质量为m1和m2的两小球（均可视为质点），挂在圆弧轨道光滑边缘C的两边，开始时m1位于C点，然后从静止释放．则（ ）
质量为m1、m2的两个星球组成双星，它们在相互之间的万有引力作用下绕两球连线上某点O做匀速圆周运动，则它们各自运动的周期T1：T2=
如图甲所示，-根轻质弹簧的两端分别与质量为m1和m2的两个物块A，B相连接，并静止在光滑的水平面上．t=0时刻，A的速度方向水平向右，大小为3m/s，两个物块的速度随时间变化的规律如图乙所示．根据图象提供的信息求：①两物块的质量之比；