��Ŀ����
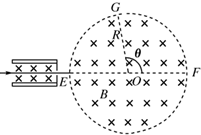
��ͼ����ʾ�������������һ����ԴA����ÿ��
��ʱ������ʱ����AO�������ⷢ��һ�����ӣ������Ҳ�Ϊһ������߽�����������ǿ�糡����ǿ�ų����������߾���ΪL��λ�ô���һӫ���������Ӵ�ӫ�����Ͻ�ʹӫ�����ϳ���һ�����㣮���ߺ�ӫ�����ƽ�У���AO��ӫ�������ֱ�����ijʱ�������˶�������λ�ÿ�ʼ��ʱ����Ϊt=0����������ͼ����ʾ�����Ա仯�ĵ硢�ų�����ǿ��С��ϵΪ
=
B������
Ϊ���ӵ�������λ��ʱ���ٶȴ�С��������t=
��ʱ�̵�������λ�õ�������t=2Tʱ�̵���ӫ�����ϵ�O�㣻��t=
ʱ�̵�������λ�õ����Ӵ�ӫ�����ϵ�P�㣬��OP֮��ľ���Ϊ
���Ը�����������ȷ����ӫ����������Щʱ�̣���ʲôλ�������ӵ��

| T |
| 2 |
| E | 0 |
| v | 0 |
| v | 0 |
| 3T |
| 2 |
| T |
| 2 |
| L |
| 2 |

����t=
ʱ�̵������ߵ�������=2Tʱ�̵���ӫ�����ϵ�O�㣬����t=
��t=2T�ڼ�糡�ʹų���Ϊ�㣬������ֱ���˶���O�㣬˵�����ӵ��������ƣ��ʣ�
��1��t=0ʱ�̽���������ܵ��ĵ糡������������ƽ�⣬��������ֱ���˶�����t=
ʱ�̵���O�㣮
��2��t=
ʱ�̽��������ֻ�ܵ糡�����ã�����ƽ���˶���t=Tʱ�̵���P�㣬OP=
��
��3��t=Tʱ�̽��������ֻ�������������ã����
x=v0?
=L
��
=
��v0T=2L
��y=
?
?(
)2=
��
=
����qv0B=m
��������R=
=L
�����ڴų����˶�������Ϊ T0=
=��T
�辭��
ʱ�伴
ʱ�������˶���F�㣬��˹���������ת����Բ�Ľ�Ϊ�ȣ���
=
����æ�=1rad
�Ժ����Ӳ�����������ֱ���˶��Ĵ�Q�㣬��QO���ľ���Ϊ
yQO=��L-Lcos�ȣ�+��L-Lsin�ȣ�tan��=��L-Lcos1��+��+��L-Lsin1��tan1��
��4��t=
ʱ�̵�������λ�õ�����������ֱ���˶���t=2Tʱ�̵���ӫ�����ϵ�O�㣻
��5���Ժ��ظ�������t=2kT��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+
��T��k=0��1��2��3������ʱ�̵���O�㣻
t=��2k+
��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+1��T��k=0��1��2��3������ʱ�̵���P�㣻
t=��2k+1��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+1��T+
+
��k=0��1��2��3������ʱ�̵���Q�㣻
t=��2k+
��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+2��T��k=0��1��2��3������ʱ�̵���O�㣮
��
t=2kT��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+
��T��k=0��1��2��3������ʱ�̵���O�㣻
t=��2k+
��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+1��T��k=0��1��2��3������ʱ�̵���P�㣻
t=��2k+1��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+1��T+
+
��k=0��1��2��3������ʱ�̵���Q�㣻
t=��2k+
��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+2��T��k=0��1��2��3������ʱ�̵���O�㣮
| 3T |
| 2 |
| 3T |
| 2 |
��1��t=0ʱ�̽���������ܵ��ĵ糡������������ƽ�⣬��������ֱ���˶�����t=
| T |
| 2 |
��2��t=
| T |
| 2 |
| L |
| 2 |
��3��t=Tʱ�̽��������ֻ�������������ã����
x=v0?
| T |
| 2 |
��
| L |
| v0 |
| T |
| 2 |
��y=
| 1 |
| 2 |
| E0q |
| m |
| T |
| 2 |
| L |
| 2 |
| m |
| E0q |
| T2 |
| 4L |
����qv0B=m
| ||
| R |
| mv0 |
| qB |
�����ڴų����˶�������Ϊ T0=
| 2��m |
| qB |
�辭��
| T |
| 2 |
| 3T |
| 2 |
| �� |
| 2�� |
| ||
| ��T |
�Ժ����Ӳ�����������ֱ���˶��Ĵ�Q�㣬��QO���ľ���Ϊ
yQO=��L-Lcos�ȣ�+��L-Lsin�ȣ�tan��=��L-Lcos1��+��+��L-Lsin1��tan1��
��4��t=
| 3T |
| 2 |
��5���Ժ��ظ�������t=2kT��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+
| 1 |
| 2 |
t=��2k+
| 1 |
| 2 |
t=��2k+1��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+1��T+
| T |
| 2 |
| L-sin1 |
| v0cos1 |
t=��2k+
| 3 |
| 2 |
��
t=2kT��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+
| 1 |
| 2 |
t=��2k+
| 1 |
| 2 |
t=��2k+1��T��k=0��1��2��3������ʱ�̵�����λ�õ����ӣ���t=��2k+1��T+
| T |
| 2 |
| L-sin1 |
| v0cos1 |
t=��2k+
| 3 |
| 2 |

��ϰ��ϵ�д�
 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
�����Ŀ