Question

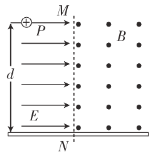
【题目】如图所示，竖直分界线左侧存在水平向右的匀强电场，电场强度大小；右侧存在垂直纸面向外的匀强磁场，磁感应强度大小。为电场中的一点，点到的距离，在其下方离点距离处有一垂直于的足够大的挡板。现将一重力不计、比荷的带正电的粒子从点由静止释放，电场和磁场的范围均足够大。求：

（1）该带电粒子运动到位置的速度大小。

（2）该带电粒子打到挡板的位置到的距离。

（3）该带电粒子从点出发至运动到挡板所用的时间。

Answer 1

【答案】(1) ；(2)0.87m；(3)

【解析】

(1) 带电粒子在电场中做匀加速直线运动，由动能定理

解得该带电粒子运动到位置的速度大小

(2)带电粒子在电场中做匀速圆周运动，由牛顿第二定律可得

解得

运动周期

在电场、磁场中的运动轨迹如图

该带电粒子打到挡板的位置到的距离

(3) 根据

解得该带电粒子在电场中运动的时间

在磁场中运动的圆弧所对的圆心角为

电荷在磁场中运动的总时间

解得

则带电粒子从P点出发至运动到挡板所需的时间为