题目内容
 (2005?河东区二模)如图是一个横截面为等腰直角三角形ABC的玻璃棱镜,其材料的折射率为n=1.6,一细束单色光从AC边上靠近A端的某点以平行于AB的方向射向棱镜,该光束射入此棱镜后可能的结果是:( )
(2005?河东区二模)如图是一个横截面为等腰直角三角形ABC的玻璃棱镜,其材料的折射率为n=1.6,一细束单色光从AC边上靠近A端的某点以平行于AB的方向射向棱镜,该光束射入此棱镜后可能的结果是:( )分析:根据折射率n=1.6,由公式sinC=
确定出临界角的范围.当光射到AB边时,根据入射角与临界角C的关系,判断能否发生全反射,若能发生全反射,依据反射定律和光路可逆性,分析出射光线与入射光线的关系.
| 1 |
| n |
解答:解:由sinC=
=
得,临界角C=arcsin
<arcsin
,则得C<45°.
设光线在AC边的折射角为r1,其入射角为i1=45°,
由n=
得,r1=arcsin
由几何知识得:光线在AB边上入射角i2=45°+r1,所以i2>C,光线在AB边上发生了全反射.
根据反射定律、几何知识得知,光线射到BC边的入射角等于AC边的折射角r1,由光路可逆性可知,光线在BC边的折射角等于AC边上入射角i1=45°,根据几何知识可知出射光线与AB边平行.故C正确,ABD错误.
故选C
| 1 |
| n |
| 1 |
| 1.6 |
| 1 |
| 1.6 |
| 1 | ||
|
设光线在AC边的折射角为r1,其入射角为i1=45°,
由n=
| sini1 |
| sinr1 |
| ||
| 3.2 |
由几何知识得:光线在AB边上入射角i2=45°+r1,所以i2>C,光线在AB边上发生了全反射.
根据反射定律、几何知识得知,光线射到BC边的入射角等于AC边的折射角r1,由光路可逆性可知,光线在BC边的折射角等于AC边上入射角i1=45°,根据几何知识可知出射光线与AB边平行.故C正确,ABD错误.
故选C
点评:本题的解题关键是掌握全反射条件、折射定律,巧妙运用光路可逆性进行判断.

练习册系列答案
相关题目
 (2005?河东区二模)1931年英国物理学家狄拉克从理论上预言,存在只有一个磁极的粒子,即“磁单极子”.1982年英国物理学家卡布莱设计了一个寻找磁单极子的实验,他设想,如果一个只有N极的磁单极子从上向下穿过一个如图所示的超导线圈,那么从上向下看,超导线圈上将出现 ( )
(2005?河东区二模)1931年英国物理学家狄拉克从理论上预言,存在只有一个磁极的粒子,即“磁单极子”.1982年英国物理学家卡布莱设计了一个寻找磁单极子的实验,他设想,如果一个只有N极的磁单极子从上向下穿过一个如图所示的超导线圈,那么从上向下看,超导线圈上将出现 ( )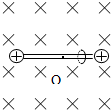 (2005?河东区二模)如图所示,两个等量的正电荷Q1、Q2固定在绝缘光滑水平面上,两点电荷用一光滑绝缘杆相连,O点为杆的中点,杆上有一带正电的小环,杆所在的区域存在一个沿水平方向且与杆垂直的匀强磁场,将小环由静止从图示位置开始释放,在小环运动过程中,下列说法中正确的是:( )
(2005?河东区二模)如图所示,两个等量的正电荷Q1、Q2固定在绝缘光滑水平面上,两点电荷用一光滑绝缘杆相连,O点为杆的中点,杆上有一带正电的小环,杆所在的区域存在一个沿水平方向且与杆垂直的匀强磁场,将小环由静止从图示位置开始释放,在小环运动过程中,下列说法中正确的是:( )