题目内容
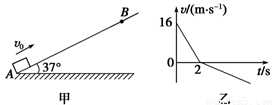
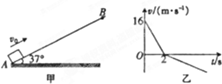
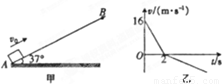
 如图甲所示,有一足够长的粗糙斜面,倾角θ=37°,一滑块以初速度v0=16m/s从底端A点滑上斜面,滑至B点后又返回到A点.滑块运动的图象如图乙所示,
如图甲所示,有一足够长的粗糙斜面,倾角θ=37°,一滑块以初速度v0=16m/s从底端A点滑上斜面,滑至B点后又返回到A点.滑块运动的图象如图乙所示,求:(已知:sin37°=0.6,cos37°=0.8,重力加速度g=10m/s2)
(1)AB之间的距离.
(2)滑块再次回到A点时的速度.
(3)滑块在整个运动过程中所用的时间.
分析:(1)速度图象与坐标轴所围“面积”等于位移,由数学知识求出位移;
(2)根据运动学公式求解出上滑过程的加速度,然后受力分析并根据牛顿第二定律列式;下滑时同样受力分析并根据牛顿第二定律列式求解加速度,然后根据运动学公式列式求解;
(3)先求解上滑的时间,再根据运动学公式求解下滑的时间,得到总时间.
(2)根据运动学公式求解出上滑过程的加速度,然后受力分析并根据牛顿第二定律列式;下滑时同样受力分析并根据牛顿第二定律列式求解加速度,然后根据运动学公式列式求解;
(3)先求解上滑的时间,再根据运动学公式求解下滑的时间,得到总时间.
解答:解:(1)由图知 S=
m=16m
(2)滑块由A到B a1=
=
=8m/s2;
上滑过程受重力、支持力和摩擦力,根据牛顿第二定律,有:
mgsinθ+μmgcosθ=ma1;
解得a1=g(sinθ+μcosθ) ①
由B到A过程,受重力、支持力和摩擦力,根据牛顿第二定律,有:
mgsinθ-μmgcosθ=ma2;
解得:a2=g(sinθ-μcosθ) ②
由以上各式得 a2=4m/s2;
vA=
=8
m/s;
(3)A到B过程,由图象得到:t1=2s;
B到A过程,由速度时间关系公式得到:t2=
=2
s
t=t1+t2=2(1+
)s
答:(1)AB之间的距离为16m;
(2)滑块再次回到A点时的速度为8
m/s;
(3)滑块在整个运动过程中所用的时间为2(1+
)s.
| 16×2 |
| 2 |
(2)滑块由A到B a1=
| △v |
| △t |
| 16 |
| 2 |
上滑过程受重力、支持力和摩擦力,根据牛顿第二定律,有:
mgsinθ+μmgcosθ=ma1;
解得a1=g(sinθ+μcosθ) ①
由B到A过程,受重力、支持力和摩擦力,根据牛顿第二定律,有:
mgsinθ-μmgcosθ=ma2;
解得:a2=g(sinθ-μcosθ) ②
由以上各式得 a2=4m/s2;
vA=
| 2a2S |
| 2 |
(3)A到B过程,由图象得到:t1=2s;
B到A过程,由速度时间关系公式得到:t2=
| vA |
| a2 |
| 2 |
t=t1+t2=2(1+
| 2 |
答:(1)AB之间的距离为16m;
(2)滑块再次回到A点时的速度为8
| 2 |
(3)滑块在整个运动过程中所用的时间为2(1+
| 2 |
点评:本题关键根据速度时间图象得到上滑时的运动情况,求解出加速度后根据牛顿第二定律确定受力情况;下滑过程是已知受力情况,求解出加速度后确定运动情况.

练习册系列答案
相关题目