题目内容
(2011?咸阳三模)如图所示,滑块A质量为2m,滑块B质量为m,滑块C的质量为0.5m,开始时,AB分别以v1,v2的速度沿光滑水平轨道向固定在右侧的挡板运动,现将C无初速度的放在B上,并与B粘合不再分开,此时A与B相距较近,B与挡板相距足够远.若B与挡板碰撞后以原速率返弹,A与B碰撞后粘合在一起,为使B能与挡板碰撞两次,v1、v2应满足什么关系?


分析:选择正确的研究对象.
根据动量守恒定律列出等式解决问题.
能够使B能与挡板碰撞两次,找出满足的条件.
根据动量守恒定律列出等式解决问题.
能够使B能与挡板碰撞两次,找出满足的条件.
解答:解:对B、C组成的系统由动量守恒定律得:
mv2=1.5mv3 ①
即v3=
v2②
要使B能与挡板碰撞两次,
v1、v3应满足关系v1≤v3③
2mv1>
mv3④
综合解得
v 1≤v2<2v1⑤
答:使B能与挡板碰撞两次,v1、v2应满足
v 1≤v2<2v1.
mv2=1.5mv3 ①
即v3=
| 2 |
| 3 |
要使B能与挡板碰撞两次,
v1、v3应满足关系v1≤v3③
2mv1>
| 3 |
| 2 |
综合解得
| 3 |
| 2 |
答:使B能与挡板碰撞两次,v1、v2应满足
| 3 |
| 2 |
点评:应用动量守恒定律时要清楚研究的对象和守恒条件.
知道碰撞后整体的速度方向为碰撞前总动量的方向.
知道碰撞后整体的速度方向为碰撞前总动量的方向.

练习册系列答案
相关题目
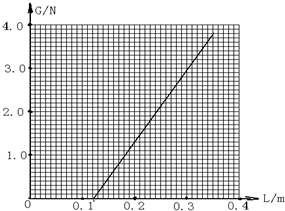 (2011?咸阳三模)某研究小组在“探究弹力和弹簧伸长关系”的实验中,将不同数量的钩碼挂在竖直弹簧下端进行测量,根据实验数据,利用描点法作出钩碼的重力G与弹簧的总长L的关系图象,如图所示
(2011?咸阳三模)某研究小组在“探究弹力和弹簧伸长关系”的实验中,将不同数量的钩碼挂在竖直弹簧下端进行测量,根据实验数据,利用描点法作出钩碼的重力G与弹簧的总长L的关系图象,如图所示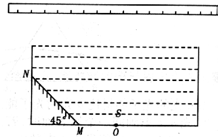 (2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n=
(2011?咸阳三模)如图所示,一不透明的圆柱形容器内装满折射率n= (2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )
(2011?咸阳三模)如图所示,一平行板电容器与电源连接,负极板B接地,以E表示两板间的电场强度,U表示电容器的电压,φp表示P的电势,闭合开关后再断开,保持正极板A不动,将负极板B向下移动一小段距离后,则( )