题目内容
如图所示,光滑竖直绝缘杆与一圆周交于B、C两点,圆心固定一电量为+Q的点电荷,一质量为m,电量为+q的环从杆上A点静止释放,已知AB=BC=h,q远小于Q,环沿绝缘杆滑到B点时的速度大小为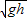 ,则( )
,则( )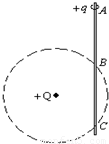
A.环在BC段的中点处加速度大小为g,方向竖直向下
B.环在B、C两点的加速度大小相等
C.环在C点的速度大小为
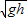
D.环从B到C的过程中,电势能先增大后减小
【答案】分析:分析环在BC段的中点处受力情况,根据牛顿第二定律求解加速度.分析环在B、C两点时的受力情况,由牛顿第二定律分析加速度的关系.环在B、C两点处电势相等,电势能相等,根据能量守恒求解环在C点的速度.根据电场力做功的正负,分析电势能的变化.
解答:解:
A、环在BC段的中点处,水平方向没有运动,加速度为零,合力为零,而竖直方向受到竖直向下的重力,则由牛顿第二定律得知,环在BC段的中点处加速度大小为g,方向竖直向下.故A正确.
B、环在B处水平方向合力为零,竖直方向受到竖直向下的重力和电场力向上的分力,而环在C处水平方向合力为零,竖直方向受到竖直向下的重力和电场力向下的分力,则由牛顿第二定律得知,环在C处加速度大于在B处的加速度.故B错误.
C、环从B运动到C点的过程中,电场力做功为零,根据能量守恒得:mgh=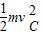 -
-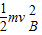 ,vB=
,vB=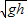 ,代入解得,vC=
,代入解得,vC=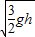 .故C错误.
.故C错误.
D、环从B到C的过程中,电场力先做负功后做正功,则环的电势能先增大后减小.故D正确.
故选AD
点评:本题求解加速度,采用力学的方法和思路,分析环的受力情况,根据牛顿第二定律求解.研究速度关系,运用能量守恒的观点进行分析,抓住B、C在同一等势面上,电势相等是关键.
解答:解:
A、环在BC段的中点处,水平方向没有运动,加速度为零,合力为零,而竖直方向受到竖直向下的重力,则由牛顿第二定律得知,环在BC段的中点处加速度大小为g,方向竖直向下.故A正确.
B、环在B处水平方向合力为零,竖直方向受到竖直向下的重力和电场力向上的分力,而环在C处水平方向合力为零,竖直方向受到竖直向下的重力和电场力向下的分力,则由牛顿第二定律得知,环在C处加速度大于在B处的加速度.故B错误.
C、环从B运动到C点的过程中,电场力做功为零,根据能量守恒得:mgh=
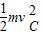 -
-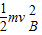 ,vB=
,vB=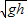 ,代入解得,vC=
,代入解得,vC=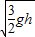 .故C错误.
.故C错误.D、环从B到C的过程中,电场力先做负功后做正功,则环的电势能先增大后减小.故D正确.
故选AD
点评:本题求解加速度,采用力学的方法和思路,分析环的受力情况,根据牛顿第二定律求解.研究速度关系,运用能量守恒的观点进行分析,抓住B、C在同一等势面上,电势相等是关键.

练习册系列答案
相关题目
 如图所示,一定质量的理想气体用不导热的活塞封闭在内壁光滑的绝热气缸内,气缸竖直放置,缸内安装一电热丝,活塞质量m,横截面积S,外界大气压强p0,重力加速度g.开始时活塞处于静止状态,将电热丝通电给气体缓慢加热,测得电热丝两端电压为U,通过的电流为I.经过时间t,活塞缓慢向上移动距离L0.求:
如图所示,一定质量的理想气体用不导热的活塞封闭在内壁光滑的绝热气缸内,气缸竖直放置,缸内安装一电热丝,活塞质量m,横截面积S,外界大气压强p0,重力加速度g.开始时活塞处于静止状态,将电热丝通电给气体缓慢加热,测得电热丝两端电压为U,通过的电流为I.经过时间t,活塞缓慢向上移动距离L0.求: 如图所示,一气缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气.现接通电源,电热丝对缸内气体缓慢加热.设活塞横截面积为S,外界大气压强为p0,电热丝热功率为P,测得通电t时间内活塞缓慢向上移动高度h,求:
如图所示,一气缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气.现接通电源,电热丝对缸内气体缓慢加热.设活塞横截面积为S,外界大气压强为p0,电热丝热功率为P,测得通电t时间内活塞缓慢向上移动高度h,求: (1)如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,下列说法正确的是
(1)如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,下列说法正确的是
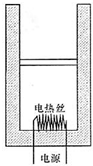 如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,大列说法正确的是( )
如图所示,一汽缸竖直放置,用一质量为m的活塞在缸内封闭了一定量的理想气体,在气缸的底部安装有一根电热丝,用导线和外界电源相连,已知气缸壁和活塞都是绝热的,气缸壁与活塞间接触光滑且不漏气,现接通电源,电热丝对缸内气体缓慢加热.关于气缸内气体,大列说法正确的是( ) 如图所示,开口向上竖直放置的内壁光滑气缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成Ⅰ、Ⅱ两部分.初状态整个装置静止不动处于平衡,Ⅰ、Ⅱ两部分气体的长度均为l0,温度为T0.设外界大气压强为P0保持不变,活塞横截面积为S,且mg=P0S,环境温度保持不变.求:
如图所示,开口向上竖直放置的内壁光滑气缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成Ⅰ、Ⅱ两部分.初状态整个装置静止不动处于平衡,Ⅰ、Ⅱ两部分气体的长度均为l0,温度为T0.设外界大气压强为P0保持不变,活塞横截面积为S,且mg=P0S,环境温度保持不变.求: