题目内容
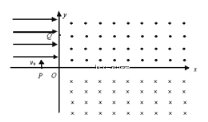
【题目】如图甲所示，两相距L=0. 5m的平行金属导轨固定于水平面上，导轨左端与阻值R=2Ω的电阻连接，导轨间虚线右侧存在垂直导轨平面的匀强磁场。质量m=0. 2kg的金属杆垂直置于导轨上，与导轨接触良好，导轨与金属杆的电阻可忽略。杆在水平向右的恒定拉力作用下由静止开始运动，并始终与导轨垂直，其v-t图像如图乙所示。在15s末时撤去拉力，同时使磁场随时间变化，从而保持回路磁通量不变，杆中电流为零。求：
（1）金属杆所受拉力的大小F；
（2）0~15s内匀强磁场的磁感应强度大小；
（3）撤去恒定拉力之后，磁感应强度随时间的变化规律.
【答案】（1）0. 24N（2）0.4T（3）
【解析】
（1）由v—t图像可知，在0～10s内，金属杆做匀加速直线运动，杆没有进入磁场，由牛顿第二定律得：
由题意可知，15s末撤去拉力，没有感应电流，杆不受安培力作用，杆所受的合外力为滑动摩擦力，由牛顿第二定律得：
，
由v—t图像可知，加速度：
解得F=0. 24N
（2）在10～15s内，金属杆做匀速直线运动，速度：t=4m/s，
金属杆受到的安培力
金属杆做匀速直线运动，处于平衡状态，由平衡条件得：
代入数据解得： 
（3）15～20s内没有产生感应电流，穿过回路的磁通量保持不变，金属杆在10～15s内的位移：
在15s后的金属杆的加速度：
，金属杆的位移：
磁通量保持不变，则：
解得
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
