题目内容
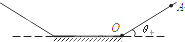 滑雪运动常在两个斜面和一个平面的组合场地中进行,我们把它简化为理想情景如图所示.假定运动员和滑板的总质量为m=60kg,从O点以初速度v0=2m/s冲上倾角为θ=37°的斜面,则经过t=5/24s时间第一次冲到斜面的最高
滑雪运动常在两个斜面和一个平面的组合场地中进行,我们把它简化为理想情景如图所示.假定运动员和滑板的总质量为m=60kg,从O点以初速度v0=2m/s冲上倾角为θ=37°的斜面,则经过t=5/24s时间第一次冲到斜面的最高点A,则求
(1)斜面的动摩擦因素;
(2)从O点出发,第一次回到O点需要的时间.(g=10m/s2)
分析:运动员沿斜面向上做匀减速运动,最后从斜面向下匀加速运动,两次经过B点.根据牛顿第二定律和运动学公式分别求出每个过程的加速度和运动时间,即可得解
解答:解:(1)运动员向上运动时的加速度:a1=
=
=-9.6m/s2负号表示方向沿斜面向下;
运动员沿斜面方向的受力:Fx=-mgsin37°-μmgcos37°=ma1
代入数据解得:μ=0.45
(2)运动员向下滑动时沿斜面方向的受力:Fx′=mgsin37°-μmgcos37°=ma2
代入数据得:a2=2.4m/s2
运动员沿斜面上升的最大高度:2a1x=0-
运动员下滑的过程:x=
a2
代入数据得:t2=
s
从O点出发,第一次回到O点需要的时间:t=t1+t2=
s=0.625s
答:(1)斜面的动摩擦因素为0.45;
(2)从O点出发,第一次回到O点需要的时间是0.625s.
| △v |
| t1 |
| 0-2 | ||
|
运动员沿斜面方向的受力:Fx=-mgsin37°-μmgcos37°=ma1
代入数据解得:μ=0.45
(2)运动员向下滑动时沿斜面方向的受力:Fx′=mgsin37°-μmgcos37°=ma2
代入数据得:a2=2.4m/s2
运动员沿斜面上升的最大高度:2a1x=0-
| v | 2 0 |
运动员下滑的过程:x=
| 1 |
| 2 |
| t | 2 2 |
代入数据得:t2=
| 5 |
| 12 |
从O点出发,第一次回到O点需要的时间:t=t1+t2=
| 15 |
| 24 |
答:(1)斜面的动摩擦因素为0.45;
(2)从O点出发,第一次回到O点需要的时间是0.625s.
点评:该题中,运动员上升的过程和下滑的过程中的加速度不同,要分别通过受力分析求得合力,然后求得加速度,再进行其他的运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
