题目内容
如图a是研究小球在斜面上平抛运动的实验装置，每次将小球从弧型轨道同一位置静止释放，并逐渐改变斜面与水平地面之间的夹角θ，获得不同的射程x，最后作出了如图b所示的x-tanθ图象，则：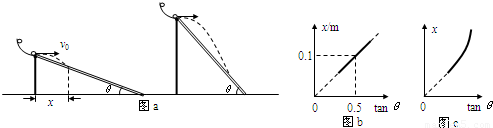
（1）由图b可知，小球在斜面顶端水平抛出时的初速度v= ．实验中发现θ超过60°后，小球将不会掉落在斜面上，则斜面的长度为 m．
（2）若最后得到的图象如图c所示，则可能的原因是（写出一个） ．
【答案】分析：（1）由平抛运动的规律列出水平位移与夹角正切值的关系，即可求得小球水平抛出时的初速度；
（2）由图c中图象可得出水平位移x随tanθ的变化关系，则可分析可能的原因．
解答：解：（1）物体在竖直方向上有：
y=
gt2
水平方向上x=vt
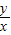=tanθ；
联立解得：
x=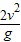
tanθ；
由图可知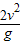
=0.2
解得：v=1m/s；
当斜面倾角θ=60°时，设斜面长度为L，有：
Lsin60°=
gt2 ①
水平方向：Lcos60°=vt ②
由①②得：
L=0.7m
（2）由图c可知，图象的斜率增大，故说明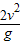
增大，因重力加速度不变，故只能说明速度增大，其原因可能为：释放位置变高或小球释放时有初速度；
故答案为：（1）1m/s；0.7 （2）释放位置变高（或小球释放时有初速度）．
点评：（1）解决本题的关键掌握平抛运动的处理方法，平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．
（2）图象法在物理学中应用较为广泛，一定要掌握图象的分析方法
（2）由图c中图象可得出水平位移x随tanθ的变化关系，则可分析可能的原因．
解答：解：（1）物体在竖直方向上有：
y=
gt2水平方向上x=vt
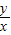=tanθ；联立解得：
x=
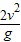tanθ； 由图可知
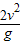=0.2解得：v=1m/s；
当斜面倾角θ=60°时，设斜面长度为L，有：
Lsin60°=
gt2 ①水平方向：Lcos60°=vt ②
由①②得：
L=0.7m
（2）由图c可知，图象的斜率增大，故说明
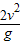增大，因重力加速度不变，故只能说明速度增大，其原因可能为：释放位置变高或小球释放时有初速度；故答案为：（1）1m/s；0.7 （2）释放位置变高（或小球释放时有初速度）．
点评：（1）解决本题的关键掌握平抛运动的处理方法，平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动．
（2）图象法在物理学中应用较为广泛，一定要掌握图象的分析方法
练习册系列答案
相关题目
（1）做“研究平抛运动”的实验时，让小球多次沿同一轨道运动，通过描点法画小球做平抛运动的轨迹，为了能准确地描绘运动轨迹，下面列出了一些操作要求，你认为正确的是
