题目内容
（12分）如图所示，质量M＝10kg、上表面光滑的足够长的木板在F＝50N的水平拉力作用下，以初速度v0=5 m/s沿水平地面向右匀速运动。现有足够多的小铁块，它们的质量均为m=1kg，将一铁块无初速地放在木板的最右端，当木板运动了L＝1m时，又无初速度地在木板的最右端放上第2块铁块，只要木板运动了L就在木板的最右端无初速度放一铁块。（取g＝10m/s2）试问：
（1）第1块铁块放上后，木板运动了L时，木板的速度多大？
（2）最终木板上放有多少块铁块？
（3）最后一块铁块与木板右端距离多远？
（1）
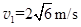（2）最终有7 块铁块放在木板上（3）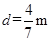
【解析】（1）木板最初做匀速运动，由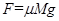
解得，
第l 块铁块放上后，木板做匀减速运动，即有：
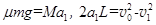代人数据解得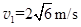： （4分）
（2）设最终有n块铁块能静止在木板上．则木板运动的加速度大小为：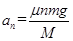
第1 块铁块放上后：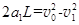
第2 块铁抉放上后：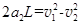
第n块铁块放上后：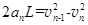
由上可得：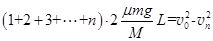
木板停下时，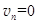
，得n=6.6。即最终有7 块铁块放在木板上。
（5分）
（3）从放上第1块铁块至刚放上第7 块铁块的过程中，由（2）中表达式可得：
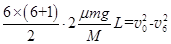
从放上第7 块铁块至木板停止运动的过程中，设木板发生的位移为d ，则：
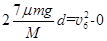联立解得：
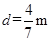（3分）
本题考查牛顿第二定律的应用，开始木板做匀速直线运动，拉力等于摩擦力，之后木板在铁块的摩擦力作用下做匀减速直线运动，可求得加速度大小，再由运动学公式可求得v1大小，第二问应用数学的归纳法求解，列出第1块、第二块…第n块放上后的位移与速度间的关系，n个式子相加可得n与初速度的关系，同理可列出第一块到第七块的位移与速度关系，从放上第7 块铁块至木板停止运动的过程中，设木板发生的位移为d，列式求解
