题目内容
如图所示，在游乐节目中，要求选手从高为
H的平台上A点由静止出发，沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出，最后刚好落到水池中的浮台上．设滑道可以伸缩，其水平距离为L，B点的高度h可由选手自由调节(取g＝10 m/s2)．要求：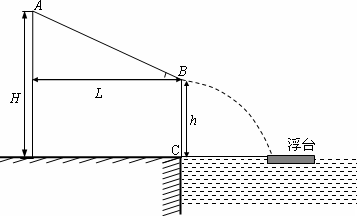
(
1)选手到达B点的速度表达式；(
2)试证明选手落到浮台上的速度大小与B点的高度h无关；(
3)同学甲认为B点的高度h越大，选手在空中飞越的时间越长，在浮台上的落点距岸边C越远；同学乙认为B点的高度h越小，选手到达B点的水平速度越大，在浮台上的落点距岸边C越远，请通过推算说明你的观点．
答案：
解析：
解析：
|
(1)由A运动到B过程，设滑道倾角为 则由牛顿定律得： 又： 且： 解得： (2)平抛运动过程： 竖直方向： 水平方向： 选手落到浮台上的速度大小： 与h无关．(1分) (3)设选手在浮台上的落点距岸边C的距离为S， 对平抛运动过程： 得： 当： 且： 因此，两人的看法均不正确． 当 当 |
，
(1分)
(1分)
(1分)
(1分)
(1分)
(1分)
(1分)
(1分)
(1分)
时，选手在浮台上的落点距岸边C的距离取最大值(1分)
(1分)
时，h越大，S越小(1分)；
时，h越小，S越小(1分)．
练习册系列答案
名校课堂系列答案
相关题目
如图所示，在游乐节目中，选手需借助悬挂在高处的绳飞越到水平的浮台上．选手可视为质量m=60kg的质点，选手抓住绳由静止开始摆动，此时绳与竖直方向夹角α=530，绳的悬挂点O距水面的高度为H=3m．不计空气阻力和绳的质量，浮台露出水面的高度不计，水足够深．g=10m/s2，sin53°=0.8，cos53°=0.6求：
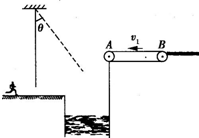如图所示，在游乐节目中，选手需要借助悬挂在高处的绳子飞越到对面的高台上．一质量m=60kg的选手脚穿轮滑鞋以v0=7m/s的水平速度抓住竖直的绳子开始摆动，选手可看作质点，绳子的悬挂点到选手的距离L=6m．当绳摆到与竖直方向夹角θ=37°时，选手放开绳子，不考虑空气阻力和绳子的质量．取重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8．
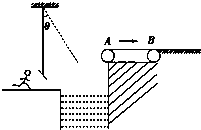如图所示，在游乐节目中，一质量为m=60kg的选手以v0=7m/s的水平速度抓住竖直绳下端的抓手开始摆动，当绳摆到与竖直方向夹角θ=37°时，选手放开抓手，松手后的上升过程中选手水平速度保持不变，运动到水平传送带左端A时速度刚好水平，并在传送带上滑行，传送带以v=2m/s匀速向右运动．已知绳子的悬挂点到抓手的距离为L=6m，传送带两端点A、B间的距离s=7m，选手与传送带的动摩擦因数为μ=0.2，若把选手看成质点，且不考虑空气阻力和绳的质量．（g=10m/s2，sin37°=0.6，cos37°=0.8）求：