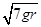题目内容
如图所示,一个半径为R的金属圆环被支架M固定在水平地面上。可视为质点的小球A、B用不可伸长的细软轻线连接,跨过圆环,A的质量为B的两倍。当B位于地面时,A恰好处于圆环的水平直径右端且离地面高为h。现将A由静止释放,B相对地面上升的最大高度是(A触地后,B上升过程中绳一直处于松弛状态)
A. B.
B. C.
C. D.h
D.h
C
解析试题分析:设B的质量为 ,则A的质量为
,则A的质量为 ,以A、B组成的系统为研究对象,在A落地前,由机械能守恒定律可得:
,以A、B组成的系统为研究对象,在A落地前,由机械能守恒定律可得: ,可得:
,可得: ;以B为研究对象,在B单独上升过程中,由机械能守恒定律可得:
;以B为研究对象,在B单独上升过程中,由机械能守恒定律可得: ,可得
,可得 ,则B上升的最大高度
,则B上升的最大高度 ,故选C。
,故选C。
考点:本题考查了机械能守恒定律。

半径为r和R(r<R)的光滑半圆形槽,其圆心在同一水平面上,如图所示,质量相等的两小球(可看成质点)分别自半圆形槽左边缘的最高点无初速释放,在下滑过程中关于两小球的说法正确的是
| A.机械能均逐渐减小 |
| B.经最低点时动能相等 |
| C.两球经过最低点时加速度大小不等 |
| D.机械能总是相等的 |
一吊篮悬挂在绳索的下端放在地面上,某人站在高处将吊篮由静止开始竖直向上提起,运动过程中,吊篮的机械能与位移的关系如图所示,其中 段图像为直线,
段图像为直线, 段图像为曲线,
段图像为曲线, 段图像为水平直线,则下列说法正确的是:( )
段图像为水平直线,则下列说法正确的是:( )
A.在 过程中,吊篮所受的拉力均匀增大 过程中,吊篮所受的拉力均匀增大 |
B.在 过程中,吊篮的动能不断增大 过程中,吊篮的动能不断增大 |
C.吊篮在 处的动能可能小于 处的动能可能小于 处的动能 处的动能 |
D.在 过程中,吊篮受到的拉力等于重力 过程中,吊篮受到的拉力等于重力 |
质量为2 kg的物体,放在动摩擦因数μ=0.1的水平面上,在水平拉力的作用下由静止开始运动,拉力做的功W随物体的位移x变化的关系如图所示.取重力加速度g=10 m/s2,则 ( )
| A.x=0至x=3 m的过程中,物体的加速度是2.5 m/s2 |
| B.x=6 m时,拉力的功率是6 W |
| C.x=9 m时,物体的速度是3 m/s |
| D.x=3 m至x=9 m过程中,合力做的功是12 J |
如图所示,ABC为竖直平面内的光滑绝缘轨道,其中AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道处在匀强磁场中,磁场方向垂直纸面向里.质量相同的甲、乙、丙三个小球中,甲球带正电、乙球带负电、丙球不带电.现将三个小球在轨道AB上分别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )
| A.甲球的释放位置比乙球的高 |
| B.运动过程中三个小球的机械能均保持不变 |
| C.经过最高点时,三个小球的速度相等 |
| D.经过最高点时,甲球的速度最小 |
水平光滑直轨道ab与半径为R的竖直半圆形光滑轨道bc相切,一小球以初速度v0沿直轨道ab向右运动,如图所示,小球进入半圆形轨道后刚好能通过最高点c。则
| A.R越大,v0越大 |
| B.R越大,小球经过b点后的瞬间对轨道的压力变大 |
| C.m越大,v0越大 |
| D.m与R同时增大,初动能Ek0增大 |




 B.最大值
B.最大值
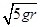 D.最大值
D.最大值