题目内容
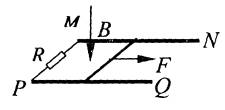
两根固定在水平面上的光滑的平行金属导轨MN和PQ,一端接有阻值为R的电阻,处于方向竖直向下的匀强磁场中。在导轨上垂直导轨跨放质量为m的金属直杆,金属杆的电阻为r,金属杆与导轨接触良好,导轨足够长且电阻不计。金属杆在垂直杆的水平恒力F作用下向右匀速运动时,电阻R上消耗的电功率是P,从某一时刻开始撤去水平力F。求撤去水平力F后;(1)通过电阻R的电流方向是:_______________________。
(2)金属杆的速度、加速度如何变化?简述原因。
(3)电阻R上产生的焦耳热是多少?
(4)当电阻R上消耗的电功率为

(1)M→P (2)速度变小,加速度变小。由于撤去水平力F,在水平方向金属杆只受安培力作用,安培力的方向与速度方向相反,所以金属杆的速度变小;由此感应电动势变小,感应电流变小,导致安培力变小,由牛顿第二定律,所以金属杆的加速度变小。(3)金属杆匀速运动,所受安培力与外力F平衡,设导轨间距为L,有: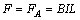 电阻消耗的功率为P,由:
电阻消耗的功率为P,由: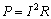 得:
得: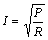 此时电路中消耗的总功率:
此时电路中消耗的总功率: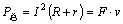 金属杆的速度
金属杆的速度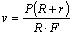 撤去力F后,整个电路中产生的热量为:
撤去力F后,整个电路中产生的热量为: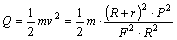 由于电流I相同,焦耳热与电阻成正比,故有:
由于电流I相同,焦耳热与电阻成正比,故有: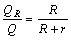 所以,撤去力F后,电阻R上产生的焦耳热为:
所以,撤去力F后,电阻R上产生的焦耳热为: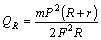 (4)撤去水平力F后,当电阻R上消耗的电功率为
(4)撤去水平力F后,当电阻R上消耗的电功率为 时,由:
时,由: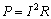 此时电流:
此时电流: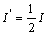 由:
由: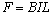 所以此时安培力:
所以此时安培力: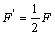 由:
由: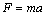 所以此时金属杆的加速度:
所以此时金属杆的加速度: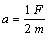 方向:水平向左
方向:水平向左

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目


 P时,金属杆的加速度大小和方向?
P时,金属杆的加速度大小和方向?
