题目内容
 如图所示,在宇宙中有一种三星系统,由三颗质量相等的恒星组成等边三角形,它们绕三角形的中心匀速转动,已知某三星系统远离其他星体,可以认为它们与其他星体的作用力为0,它们之间的距离均为r,绕中心转动周期为T,每颗星均可看作质点.试求这三颗星的总质量.
如图所示,在宇宙中有一种三星系统,由三颗质量相等的恒星组成等边三角形,它们绕三角形的中心匀速转动,已知某三星系统远离其他星体,可以认为它们与其他星体的作用力为0,它们之间的距离均为r,绕中心转动周期为T,每颗星均可看作质点.试求这三颗星的总质量.分析:先写出任意两个恒星之间的万有引力,求每一颗恒星受到的合力,该合力提供它们的向心力.然后用r表达出它们的轨道半径,最后写出用周期表达的向心力的公式,整理即可的出结果.
解答: 解:设这三颗星分别为A、B、C,其质量分别为MA、MB、MC,且MA=MB=MC=M,A的受力如右图所示,因为A 做匀速圆周运动,
解:设这三颗星分别为A、B、C,其质量分别为MA、MB、MC,且MA=MB=MC=M,A的受力如右图所示,因为A 做匀速圆周运动,
对A 有:FBAcos30°+FCAcos30°=MAω2rOA
而 ω=
由万有引力定律知:则FBA=FCA=G
由几何知识得 rOA=
?
r=
r
所以 2G
cos30°=M
?
r
解得:M=
,所以三颗星的总质量为3M=
答:这三颗星的总质量是
.
 解:设这三颗星分别为A、B、C,其质量分别为MA、MB、MC,且MA=MB=MC=M,A的受力如右图所示,因为A 做匀速圆周运动,
解:设这三颗星分别为A、B、C,其质量分别为MA、MB、MC,且MA=MB=MC=M,A的受力如右图所示,因为A 做匀速圆周运动,对A 有:FBAcos30°+FCAcos30°=MAω2rOA
而 ω=
| 2π |
| T |
由万有引力定律知:则FBA=FCA=G
| M2 |
| r2 |
由几何知识得 rOA=
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
所以 2G
| M2 |
| r2 |
| 4π2 |
| T2 |
| ||
| 3 |
解得:M=
| 4π2r3 |
| 3GT2 |
| 4π2r3 |
| GT2 |
答:这三颗星的总质量是
| 4π2r3 |
| GT2 |
点评:解决该题首先要理解模型所提供的情景,然后能够列出合力提供向心力的公式,才能正确解答题目.

练习册系列答案
相关题目






 注入人体,
注入人体,
 D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
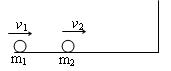
 ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小. D.液体表面层的分子比液体内部的分子有更大的分子势能
D.液体表面层的分子比液体内部的分子有更大的分子势能 D.超声波可以在真空中传播
D.超声波可以在真空中传播
 注入人体,
注入人体, ⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.
⑶如图所示,质量分别为m1和m2的两个小球在光滑水平面上分别以速度v1、v2同向运动,并发生对心碰撞,碰后m2被右侧墙壁原速弹回,又与m1碰撞,再一次碰撞后两球都静止.求第一次碰后m1球速度的大小.