Question

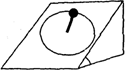（2011?保定模拟）如图所示，在倾角是30°的光滑斜面上，有一长为l的轻杆，杆的一端固定着一个小球，另一端绕垂直于斜面的光滑轴做圆周运动，运动到最高点速度是

gl

．（　　）

• A．在最高点时，杆对球的作用力为0
• B．在最高点时，杆对球的作用力沿杆向上
• C．在最高点时，杆对球的作用力沿杆向下
• D．在最低点时，杆对球的作用力沿杆向上，大小是

  7

  2

  mg

Answer 1

分析：将重力按照作用效果沿平行斜面和垂直斜面方向正交分解，小球转动过程中，只有重力做功，机械能守恒；根据合力提供向心力列式求解；

解答：解：A、B、C、将重力按照作用效果沿平行斜面和垂直斜面方向正交分解，在最高点，重力的下滑分量和杆弹力的合力提供向心力，假设弹力为拉力，有
mgsinθ+F=m

v2

l

v=

gl

解得
F=mg-mgsinθ=

1

2

mg＞0
故假设成立，杆对球为拉力；
故A错误、B错误、C正确；
D、小球从最高点到最低点过程，机械能守恒，有

1

2

mv2+mg(2lsinθ)=

1

2

m

v

2 2

   ①
在最低点，有
F′-mgsinθ=m

v 2 2

l

    ②
由①②解得
F′=

7

2

mg
故D正确；
故选CD．

点评：本题关键先将重力按照作用效果正交分解，由于合力提供向心力，然后根据牛顿第二定律和机械能守恒定律列式求解．