题目内容
19.某同学安装如图甲的实验装置,验证机械能守恒定律.如图乙是该实验得到的一条点迹清晰的纸带,现要取A、B两点来验证实验,已知电火花打点计时器每隔0.02S打一个点.
请回答下列问题:
①电火花打点计时器的工作电压是220V;
②根据纸带可以判断,实验时纸带的左端是和重物相连接(选填“左”或“右”);
③若X2=4.80cm,则在纸带上打下计数点B时的速度VB=1.20m/s(计算结果保留三位有效数字);
④若X1数据也已测出,则实验还需测出的物理量为AB之间的距离.
分析 解决实验问题首先要掌握该实验原理,了解实验的仪器、操作步骤和数据处理以及注意事项.
纸带实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答 解:①电火花打点计时器的工作电压是220V,
②从纸带上可以发现从左到右,相邻的计数点的距离越来越大,也就是说明速度越来越大.
与重物相连接的纸带先打出点,速度较小,所以实验时纸带的左端通过夹子和重物相连接.
③利用匀变速直线运动的推论得:
vB=$\frac{{x}_{2}}{2T}$=$\frac{0.048}{2×0.02}$=1.20m/s
④要验证机械能守恒定律,则要求出重力势能的变化量,所以还要测出AB之间的距离;
故答案为:①220V
②左
③1.20
④AB之间的距离
点评 纸带问题的处理是力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
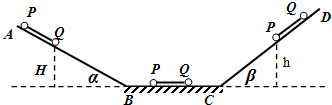
7.如图所示,ABCD是一段竖直平面内的光滑轨道,AB段与水平面成α角,CD段与水平面成β角,其中BC段水平,且其长度大于L.现有两小球P、Q,质量分别是3m、2m,用一长为L的轻质直杆连接,将P、Q由静止从高H处释放,在轨道转折处用光滑小圆弧连接,不考虑两小球在轨道转折处的能量损失,则小球P滑上CD轨道的最大高度h为( )

| A. | h=H | B. | h=H+Lsinβ | ||
| C. | h=H+$\frac{L(sinα-sinβ)}{5}$ | D. | h=H+$\frac{L(3sinα-2sinβ)}{5}$ |
10. 如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力f的作用.已知F1=10N,F2=2N,则木块受到的摩擦力大小和方向分别为( )
如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力f的作用.已知F1=10N,F2=2N,则木块受到的摩擦力大小和方向分别为( )
 如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力f的作用.已知F1=10N,F2=2N,则木块受到的摩擦力大小和方向分别为( )
如图所示,静止在水平桌面上的木块,在水平方向受到推力F1、F2和摩擦力f的作用.已知F1=10N,F2=2N,则木块受到的摩擦力大小和方向分别为( )| A. | 8N 水平向右? | B. | 8N 水平向左 | C. | 10N 水平向右? | D. | 12N 水平向左 |
7.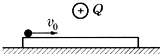 如图所示,在水平放置的光滑金属板中点的正上方,有带正电的点电荷Q.一表面绝缘、带正电的金属球(可视为质点,且不影响原电场)以速度v0开始在金属板上向右运动,在运动过程中( )
如图所示,在水平放置的光滑金属板中点的正上方,有带正电的点电荷Q.一表面绝缘、带正电的金属球(可视为质点,且不影响原电场)以速度v0开始在金属板上向右运动,在运动过程中( )
 如图所示,在水平放置的光滑金属板中点的正上方,有带正电的点电荷Q.一表面绝缘、带正电的金属球(可视为质点,且不影响原电场)以速度v0开始在金属板上向右运动,在运动过程中( )
如图所示,在水平放置的光滑金属板中点的正上方,有带正电的点电荷Q.一表面绝缘、带正电的金属球(可视为质点,且不影响原电场)以速度v0开始在金属板上向右运动,在运动过程中( )| A. | 小球减速后作加速运动 | B. | 小球作匀速直线运动 | ||
| C. | 小球受电场力的冲量为零 | D. | 以上说法可能都不正确 |
4.如图甲所示,物体以一定的初速度从倾角α=37°的斜面底端沿斜面向上运动,上升的最大高度为3.0m.选择地面为参考平面,上升过程中,物体的机械能E随高度h的变化图象如图乙所示.g=10m/s2,sin37°=0.60,cos37°=0.80.则( )


| A. | 物体上升过程的加速度大小a=10m/s2 | |
| B. | 物体与斜面间的动摩擦因数μ=0.40 | |
| C. | 物体的质量m=0.67kg | |
| D. | 物体回到斜面底端时的动能Ek=10J |
8.联合国宣布2015年为“光和光基技术国际年”(国际光学年).下列关于光科学发展历史上的一系列说法,符合事实的是( )
| A. | 1865年麦克斯韦提出光是电磁波的一种形态 | |
| B. | 1801年托马斯•杨在实验室成功观察到了光的衍射 | |
| C. | 1818年泊松通过实验发现了圆板衍射的“泊松亮斑” | |
| D. | 1905年爱因斯坦在广义相对论中提出光速不变原理 |
9. 一列简谐横波沿x轴正方向传播在t=0时刻的波形如图.已知这列波在P点处依次出现两个波峰的时间间隔为0.4s,Q为x=9m处的一点.以下说法正确的是( )
一列简谐横波沿x轴正方向传播在t=0时刻的波形如图.已知这列波在P点处依次出现两个波峰的时间间隔为0.4s,Q为x=9m处的一点.以下说法正确的是( )
 一列简谐横波沿x轴正方向传播在t=0时刻的波形如图.已知这列波在P点处依次出现两个波峰的时间间隔为0.4s,Q为x=9m处的一点.以下说法正确的是( )
一列简谐横波沿x轴正方向传播在t=0时刻的波形如图.已知这列波在P点处依次出现两个波峰的时间间隔为0.4s,Q为x=9m处的一点.以下说法正确的是( )| A. | 这列波的波长是5m | |
| B. | 这列波的波速是10m/s | |
| C. | 质点Q需要再经过0.7s,才能第一次到达波峰处 | |
| D. | 质点Q达到波峰时,质点P恰好到达波谷处 |
 如图所示,黑箱内有导线、定值电阻和两只电压恒定的电池组成的电路.今用R=10Ω的电阻分别接在1、2和3、4之间,测得电流I12=0.4A,I34=0;而将此电阻R分别接在其它任意两点之间时,通过R的电流均为I=0.1A,画出有关电路图(标出元件的参数)
如图所示,黑箱内有导线、定值电阻和两只电压恒定的电池组成的电路.今用R=10Ω的电阻分别接在1、2和3、4之间,测得电流I12=0.4A,I34=0;而将此电阻R分别接在其它任意两点之间时,通过R的电流均为I=0.1A,画出有关电路图(标出元件的参数)