题目内容
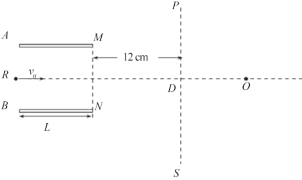
【题目】一束初速度不计的电子在经U的加速电压加速后，在距两极板等距处垂直进入平行板间的匀强电场，如图所示。若板间距离d，板长l，偏转电极边缘到荧光屏的距离为L，偏转电场只存在于两个偏转电极之间。已知电子质量为m，电荷量为e，求：
（1）电子离开加速电场是的速度大小；
（2）电子经过偏转电场的时间；
（3）要使电子能从平行板间飞出，两个极板上最多能加多大电压？
（4）电子最远能够打到离荧光屏上中心O点多远处？
【答案】（1）v0=
（2）t=
（3）U′=
（4）Y=
【解析】（1）设电子流经加速电压后的速度为v0，则由动能定理有：
qU=
mv02
又 q=e
得：v0=
（2）电子经过偏转电场时做类平抛运动，运动时间为：
t=
（3）设两极板上最多能加的电压为U′，要使电子能从平行板间飞出则电子的最大侧移量为
，则有：
=
又a=
联立以上三式得：U′=
（4）从板边缘飞出到荧光屏上离O点最远。这时
速度偏向角的正切tan α=
而vy=at
则得 tan α=
离O点最远距离为Y′+d
联立得：Y=
练习册系列答案
相关题目
