题目内容
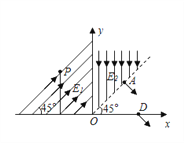
【题目】（12分）位于竖直平面内的直角坐标系xOy，，x轴沿水平方向，第一象限的角平分线OA的上方存在有界匀强电场，场强
，方向竖直向下，第二象限内有另一匀强电场
，电场方向与x轴正方向成45°角斜向上，如图所示。有一质量为m、电量为+q的带电小球在水平细线的拉力作用下恰好静止在坐标（-l，6l）处。现剪断细线，小球从静止开始运动，先后经过两电场后，从A点进入无电场区域，，最终打在x轴上D点，已知重力加速度为g，试求:
(1)电场
的场强；
(2))A点的位置坐标；
(3)到达D点时小球的动能。
【答案】(1) 
(2) (2l,2l) (3)19mgl
【解析】（1）小球在第二象限内静止，则有
解得
（2）设进入第一象限的初速度为
，在在第二象限内由动能定理可得
解得
设A点的坐标为（x，y），由于A点在象限角平分线上，则有y=x
小球进入电场，做类平抛运动，
由以上各式可得
A点的位置坐标（2l ，2l）
（3）从P到D全过程运用动能定理得
练习册系列答案
名校课堂系列答案
相关题目
