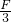题目内容
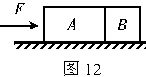
质量为2m的物体A与水平面间的摩擦可以忽略不计，质量为m的物体B与地面的动摩擦因数为μ．A、B并排放置在水平面上，用在水平推力F的作用下，共同向右做加速运动．此时（ ）分析：先对B研究：分析受力，根据牛顿第二定律判断推力与摩擦力的大小关系；然后对整体，再对B根据牛顿第二定律求出A对B的推力；
解答：解：设A对B的推力为N．
A、由题意，B向右加速运动，具有向右的加速度，B所受的滑动摩擦力大小为μmg，方向向左，则根据牛顿第二定律得知合外力向右，所以A对B的推力一定大于μmg．故A错误．
B、若μ=0，根据牛顿第二定律得：
对整体：a=
，
对B：A对B的推力N=ma=
≠0．故B错误．
C、D对整体，则有：F-μmg=3ma，得F=μmg+3ma
对B；N-μmg=ma，得N=μmg+ma
若μ=0，联立解得，N=
；若μ≠0，解得，N＞
．故C错误，D正确．
故选D
A、由题意，B向右加速运动，具有向右的加速度，B所受的滑动摩擦力大小为μmg，方向向左，则根据牛顿第二定律得知合外力向右，所以A对B的推力一定大于μmg．故A错误．
B、若μ=0，根据牛顿第二定律得：
对整体：a=
| F |
| 3m |
对B：A对B的推力N=ma=
| F |
| 3 |
C、D对整体，则有：F-μmg=3ma，得F=μmg+3ma
对B；N-μmg=ma，得N=μmg+ma
若μ=0，联立解得，N=
| F |
| 3 |
| F |
| 3 |
故选D
点评：本题运用整体法和隔离法结合研究连接体问题，考查灵活选择研究对象的能力．
练习册系列答案
相关题目
，在水平向右推力F的作用下，A、B一起向右做匀加速运动， 求:
（2）A对B的作用力为多少?
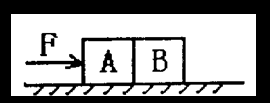
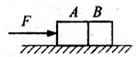质量为2m的物体A与水平面间的摩擦可以忽略不计，质量为m的物体B与地面的动摩擦因数为μ．A、B并排放置在水平面上，用在水平推力F的作用下，共同向右做加速运动．此时
