Question

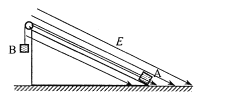
【题目】如图所示，ABC为直角三棱镜，∠A=30°，∠B=90°，斜边AC长为L．一束单色光斜射到BC的中点D，折射光线刚好与AC平行，且折射光线照射到AB边刚好发生全反射。已知光在真空中的传播速度为c，求：

①光在BC面上的入射角的正弦值；

②光线在棱镜中从D点到第一次传播到AC边所用的时间。

Answer 1

【答案】①②

【解析】

①由于折射光线DE与AC平行，因此光线在AB面上的入射角为60°，反射角也为60°。

由于折射光线DE在AB面上刚好发生全反射，则临界角C=60°

所以棱镜的折射率为：n===

设光线在BC面的入射角为i，折射角为r，由几何关系可知r =30°

根据折射定律得：n=

可得：sini=

②由几何关系得：DE=AC=L

AE=ACcos30°=L

EF==L

光在棱镜中的传播速度为：v==

因此，光线在棱镜中从D点到第一次传播到AC边所用的时间为：t==。