��Ŀ����
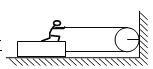
����Ŀ����ͼ��������m��0.1kg��Բ�����ڹ̶���ˮƽֱ���ϣ�Բ����ֱ���Դ��ڸ˵Ľ���ֱ����Բ����˼䶯Ħ����������0.8����Բ��ʩ��һλ����ֱƽ������˼н�Ϊ��б���ϵ�����F��

��1��������53��ʹԲ����a��4.4m/s2�ļ��ٶ��ظ��˶�����F�Ĵ�С��ȡsin53�㣽0.8��cos53�㣽0.6��
��2������F��Ϊ��˼н�Ϊ��б���¡�������ijһ�ǶȺ���������F���������Բ�������ʱ����Сֵ�����С�
���𰸡���1��1N��2��![]()
��������
��1������Բ�����������������ţ�ٵڶ����ɺ�Ħ������ʽ�����F�Ĵ�С��
��2����������F���������Բ����˵��F��ˮƽ�������������Ħ����������ƽ���������ٽ�������Ͻ��
��1����![]() ����ʱ��������ͼ����ţ�ٵڶ����ɵã�
����ʱ��������ͼ����ţ�ٵڶ����ɵã�

ˮƽ�����У�![]()
��ֱ�����У�![]()
��ã�![]() ��
��
����![]() ����ʱ������ͼ����ţ�ٵڶ����ɣ�
����ʱ������ͼ����ţ�ٵڶ����ɣ�

ˮƽ�����У� ![]()
ˮƽ�����У� ![]()
�õ���![]() ��������
��������
��������������![]() ��
��
��2������֪����������F���������Բ����Ӧ���㣺![]()
��ֱ�����У� ![]()
��![]()
��Ϊ![]()
��![]() ����������F���������Բ��
����������F���������Բ��
��![]() ����������Сֵ������Ϊ
����������Сֵ������Ϊ![]() ��
��

��ϰ��ϵ�д�
 ����������ϵ�д�
����������ϵ�д� �Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�Ż���ҵ�Ϻ��Ƽ����׳�����ϵ�д�
�����Ŀ