题目内容
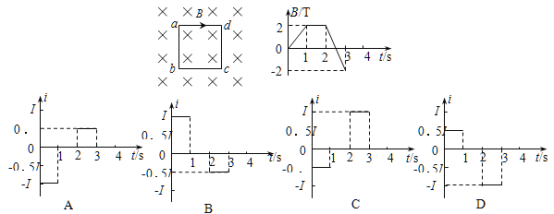
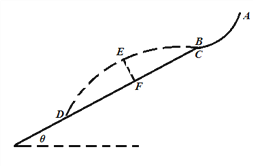
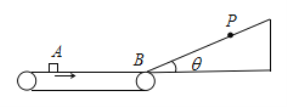
【题目】如图所示,足够长的浅色传送带以速度![]() 顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量
顺时针匀速转动,表面粗糙,传送带的右端有一固定的斜面,斜面底端B与传送带经一长度可忽略的光滑圆弧连接.现将一质量![]() 的墨色小滑块从距离B点
的墨色小滑块从距离B点![]() 的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为
的A处轻轻无初速放上传送带,已知小滑块与传送带间的动摩擦因数为![]() ,斜面倾角
,斜面倾角![]() ,斜面足够长,滑块与斜面的动摩擦因数
,斜面足够长,滑块与斜面的动摩擦因数![]() ,重力加速度g=10m/s2,
,重力加速度g=10m/s2, ![]() ,求:
,求:
(1)小滑块在传送带上留下的划痕长度![]() ;
;
(2)小滑块第一次滑上斜面后能够到达的最高点P距B点的距离![]() ;
;
(3)小滑块第二次冲上斜面时的速度大小.
【答案】(1)8m(2)3.3m(3)4m/s
【解析】
(1)小滑块在传送带上先加速运动,设加速度为a1,则![]() ...........①
...........①
加速至v0=8m/s,发生的位移![]() ............②
............②
此时传送带发生的位移.![]() ...........③
...........③
故划痕的长度![]() ...........③
...........③
(3)由于小滑块滑上斜面时做减速运动,设加速度大小为a2,由牛顿运动定律可得![]() ........④
........④
![]() .....⑤
.....⑤
联立解得![]()
(3)由于![]() ,所以滑块到达最高点后会向下加速运动,返回斜面底端,设滑块第一次滑上斜面时的最大位移为L1,第一次返回斜面底端时的速度为v1
,所以滑块到达最高点后会向下加速运动,返回斜面底端,设滑块第一次滑上斜面时的最大位移为L1,第一次返回斜面底端时的速度为v1
由牛顿运动定律可得:![]()
![]()
两式联立可得![]()
滑块返回斜面底端后,在传送带上做类竖直上抛运动,返回斜面底端时速度仍然为v1
所以,![]()

练习册系列答案
相关题目