题目内容
(10分)如图所示,在一个大小为 V/m,方向水平向左的匀强电场中,有一个小物块,质量为
V/m,方向水平向左的匀强电场中,有一个小物块,质量为 80g,带正电荷
80g,带正电荷 ,与水平轨道之间的动摩擦因数
,与水平轨道之间的动摩擦因数 0.2,在水平轨道的末端
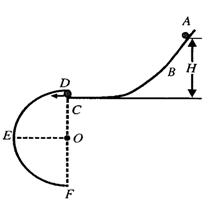
0.2,在水平轨道的末端 处,连接一个光滑的半圆形轨道,半径为
处,连接一个光滑的半圆形轨道,半径为 40cm,取
40cm,取 10m/s2,求:
10m/s2,求:
(1)若小物块恰好运动到轨道的最高点,那么小物块应该从水平轨道的哪个位置释放?
(2)如果在第(1)问的位置释放小物块,当它运动到 (轨道中点)点时对轨道的压力等于多少?
(轨道中点)点时对轨道的压力等于多少?
(1)20N (2)3.0N
解析试题分析:(1)物块能通过轨道最高点的临界条件是 解得v="2m/s" (2分)
解得v="2m/s" (2分)
设小物块释放位置距 处为
处为 ,则由动能定理
,则由动能定理 (2分)
(2分)
解得 ,即小物块应该从在水平位置距
,即小物块应该从在水平位置距 处为20m处开始释放(1分)
处为20m处开始释放(1分)
(2)P点到最高点由动能定理: (2分)
(2分)
物块到P点时, (2分)
(2分)
解得 由牛顿第三运动定律可得物块对轨道的压力为3.0N(1分)...
由牛顿第三运动定律可得物块对轨道的压力为3.0N(1分)...
考点:本题利用物体在电场中的圆周运动考查向心力公式和动能定理的综合应用,要理解题目中恰好通过最高点的含义是重力提供向心力,可以求出在最高点的速度,再结合动能定理求解.

练习册系列答案
相关题目




 ,半径分别为
,半径分别为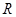 和
和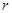 ,两板之间用一根长
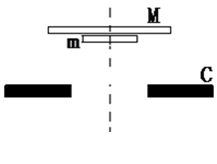
,两板之间用一根长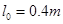 的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度
的轻绳将薄板中心相连结(未画出).开始时,两板水平放置并叠合在一起,静止于距离固定支架C高度 处. 然后自由下落到C上,支架上有一半径为
处. 然后自由下落到C上,支架上有一半径为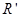 (
(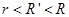 )的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,
)的圆孔,圆孔与两薄板中心均在圆板中心轴线上. 薄板M与支架发生没有机械能损失的碰撞(碰撞时间极短). 碰撞后,两板即分离,直到轻绳绷紧.在轻绳绷紧的瞬间,两板立即具有共同速度.不计空气阻力,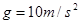 ,求:
,求: