题目内容
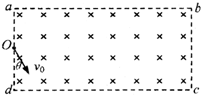一足够长的矩形区域abcd内充满磁感应强度为B，方向垂直纸面向里的匀强磁场，矩形区域的左边界ad宽为L，现从ad中点O垂直于磁场射入一带电粒子，速度大小为v0方向与ad边夹角为30°，如图所示．已知粒子的电荷量为q，质量为m（重力不计）．（1）若粒子带负电，且恰能从d点射出磁场，求v0的大小；
（2）若粒子带正电，使粒子能从ab边射出磁场，求v0的取值范围以及引范围内粒子在磁场中运动时间t的范围．
分析：（1）根据牛顿第二定律，由洛伦兹力提供向心力，结合几何关系可确定半径的范围，即可求解；
（2）根据题意确定运动轨迹，再由圆心角与周期公式，即可确定最长运动的时间；根据半径公式与半径的取值，即可求解．
（2）根据题意确定运动轨迹，再由圆心角与周期公式，即可确定最长运动的时间；根据半径公式与半径的取值，即可求解．
解答：（1）由图可知：R=
据洛伦兹力提供向心力，得：qvB=
则v0=
=
（2）当v0最大时：R1-R1cos60°=
得R1=L
则：vmax=
=
当v0最小值：R2+R2sin30°=
得：R2=
则vmin=
=
＜v0≤
带电粒子从ab边射出磁场，当速度为vmax时，运动时间最短．
tmin=
T=
速度为vmin时运动时间最长：tmax=
T=
∴粒子运动时间t的范围
≤t＜
答：（1）粒子带负电，且恰能从d点射出磁场，v0=
；
（2）粒子带正电，使粒子能从ab边射出磁场，v0的取值范围
＜v0≤
，粒子在磁场中运动时间t的范围
≤t＜
．
| L |
| 2 |
据洛伦兹力提供向心力，得：qvB=
m
| ||
| R |
则v0=
| qBR |
| m |
| qBL |
| 2m |
（2）当v0最大时：R1-R1cos60°=| L |
| 2 |
得R1=L
则：vmax=
| qBR1 |
| m |
| qBL |
| m |
当v0最小值：R2+R2sin30°=
| L |
| 2 |
得：R2=
| L |
| 3 |
则vmin=
| qBR2 |
| m |
| qBL |
| 3m |
| qBL |
| 3m |
| qBL |
| m |
带电粒子从ab边射出磁场，当速度为vmax时，运动时间最短．
tmin=
| 150° |
| 360° |
| 5πm |
| 6qB |
速度为vmin时运动时间最长：tmax=
| 240° |
| 360° |
| 4πm |
| 3qB |
∴粒子运动时间t的范围
| 5πm |
| 6qB |
| 4πm |
| 3qB |
答：（1）粒子带负电，且恰能从d点射出磁场，v0=
| qBL |
| 2m |
（2）粒子带正电，使粒子能从ab边射出磁场，v0的取值范围
| qBL |
| 3m |
| qBL |
| m |
| 5πm |
| 6qB |
| 4πm |
| 3qB |
点评：考查牛顿第二定律的应用，掌握几何关系在题中的运用，理解在磁场中运动时间与圆心角的关系．注意本题关键是画出正确的运动轨迹．
练习册系列答案
相关题目
选做题．在以下两题中选择一题完成．多做不加分
如图，一足够长的固定斜面与水平方向成α=37？角，空间有垂直于斜面的无限多个匀强磁场，其磁感应强度的大小均为B=0.5T，相邻磁场区域的磁场方向相反．每个磁场区域的宽度均为L1=0.1m，磁场区的边界均与斜面底边平行．现有一质量为m=0.05kg、电阻为R=0.5Ω的矩形金属框abcd沿此斜面下滑，已知ad=L1=0.1m，ab=L2=0.2m，下滑过程中，金属框的ab边始终与斜面底边平行，金属框与斜面间的动摩擦因数为μ=0.2，金属框下滑距离s=3m时速度达到最大，求：
选做题．在以下两题中选择一题完成．多做不加分