题目内容
（2012?聊城模拟）如图所示，质量为M 的小车放在光滑的水平面上．小车上用细线悬吊一质量为m的小球，M＞m．现用一力F水平向右拉小球，使小球和车一起以加速度a向右运动时，细线与竖直方向成α角，细线的拉力为T；若用另一力F′水平向左拉小车，使小球和车一起以加速度a′向左运动时，细线与竖直方向也成α角，细线的拉力为T′．则（ ）分析：先对左图中情况下的整体受力分析，运用牛顿第二定律列式；然后对小球受力分析，运用牛顿第二定律列式，求出绳子的拉力T和加速度a；再次对右图中的小球受力分析，运用牛顿第二定律求出绳子的拉力T′和加速度a′；最后再比较结果即可．
解答：解：先对左图中情况下的整体受力分析，受重力、支持力和拉力
根据牛顿第二定律，有
F=（M+m）a ①
再对左图中情况下的小球受力分析，如图
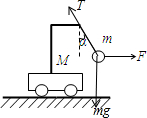
根据牛顿第二定律，有
F-Tsinα=ma ②
Tcosα-mg=0 ③
由以上三式可解得
T=
a=
再对右图中小球受力分析，如图
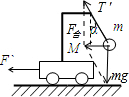
由几何关系得：
F合=mgtanα
T′=
再由牛顿第二定律，得到
a′=gtanα
由于M＞m，故a′＞a，T′=T
故选：B．
根据牛顿第二定律，有
F=（M+m）a ①
再对左图中情况下的小球受力分析，如图
根据牛顿第二定律，有
F-Tsinα=ma ②
Tcosα-mg=0 ③
由以上三式可解得
T=
| mg |
| cosα |
a=
| mgtanα |
| M |
再对右图中小球受力分析，如图
由几何关系得：
F合=mgtanα
T′=
| mg |
| cosα |
再由牛顿第二定律，得到
a′=gtanα
由于M＞m，故a′＞a，T′=T
故选：B．
点评：本题关键要多次对小球和整体受力分析，求出合力，得出加速度和绳子拉力进行比较．
练习册系列答案
阅读快车系列答案
相关题目
（2012?聊城模拟）某同学在做“探究弹力和弹簧伸长的关系”的实验时，将一轻弹簧竖直悬挂并让其自然下垂，测出其自然长度；然后在其下部施加外力F，测出弹簧的总长度L，改变外力F的大小，测出几组数据，作出外力F与弹簧总长度L的关系图线如图所示．（实验过程是在弹簧的弹性限度内进行的）由图可知该弹簧的自然长度为
（2012?聊城模拟）如图所示，一水平传送装置由轮半径均为R=