题目内容
如图所示,水平面上固定一轨道,轨道所在平面与水平面垂直,其中bcd是一段以O为圆心、半径为R的圆弧,c为最高点,弯曲段abcde光滑,水平段ef粗糙,两部分平滑连接,a、O与ef在同一水平面上.可视为质点的物块静止于a点,某时刻给物块一个水平向右的初速度,物块沿轨道经过c点时,受到的支持力大小等于其重力的 倍,之后继续沿轨道滑行,最后物块停在轨道的水平部分ef上的某处.已知物块与水平轨道ef的动摩擦因数为μ,重力加速度为g.求:
倍,之后继续沿轨道滑行,最后物块停在轨道的水平部分ef上的某处.已知物块与水平轨道ef的动摩擦因数为μ,重力加速度为g.求: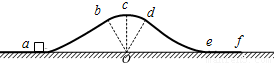
(1)物块经过c点时速度v的大小;
(2)物块在a点出发时速度v的大小;
(3)物块在水平部分ef上滑行的距离x.
【答案】分析:(1)物块在c点靠重力和支持力的合力提供向心力,根据牛顿第二定律求出c点的速度大小.
(2)通过c点的速度,对a到c段,运用机械能守恒定律求出初速度的大小.
(3)对全过程运用动能定理,求出物块A在水平轨道上滑行的距离.
解答:解:(1)在c点对物块受力分析,根据牛顿运动定律: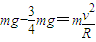
解得: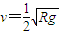
(2)物块A从a到c,根据机械能守恒定律:
解得: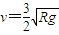
(3)设物块A在水平轨道上滑行的距离为x,从e到f,根据动能定理: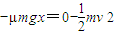
解得: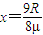 .
.
答:(1)物块经过c点时速度v的大小为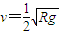 .
.
(2)物块在a点出发时速度v的大小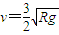 .
.
(3)物块在水平部分ef上滑行的距离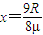 .
.
点评:本题综合考查了动能定理、机械能守恒定律以及牛顿第二定律,难度不大,关键是选择合适的研究过程,运用动能定理进行解题.
(2)通过c点的速度,对a到c段,运用机械能守恒定律求出初速度的大小.
(3)对全过程运用动能定理,求出物块A在水平轨道上滑行的距离.
解答:解:(1)在c点对物块受力分析,根据牛顿运动定律:
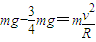
解得:
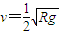
(2)物块A从a到c,根据机械能守恒定律:

解得:
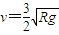
(3)设物块A在水平轨道上滑行的距离为x,从e到f,根据动能定理:
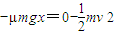
解得:
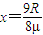 .
.答:(1)物块经过c点时速度v的大小为
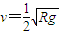 .
.(2)物块在a点出发时速度v的大小
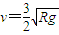 .
.(3)物块在水平部分ef上滑行的距离
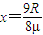 .
.点评:本题综合考查了动能定理、机械能守恒定律以及牛顿第二定律,难度不大,关键是选择合适的研究过程,运用动能定理进行解题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 如图所示,两块固连在一起的物块a和b,质量分别是ma和mb.放在水平光滑桌面上,现同时施给他们方向如图所示的推力Fa和拉力Fb,已知Fa>Fb,则a对b的作用力( )
如图所示,两块固连在一起的物块a和b,质量分别是ma和mb.放在水平光滑桌面上,现同时施给他们方向如图所示的推力Fa和拉力Fb,已知Fa>Fb,则a对b的作用力( )



