题目内容
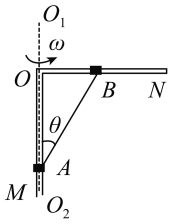
【题目】如图所示，竖起平面内的四分之一光滑圆弧轨道AB与水平直轨道BD相切于B点，轨道D端固定一竖起挡板。圆弧轨道的圆心为O、半径为R，轨道BC段光滑且长度大于
,CD段粗糙且长度为R.质量均为m的P、Q两个小球用轻杆连接，从图示位置由静止释放，Q球与档板碰撞后反向弹回，每次碰撞后瞬间P、Q两球的总动能均为碰撞前瞬间的
.Q球第一次反弹后，P球沿轨道AB上升的最大高度为
,重力加速度为g.求：
（1）P球第一次运动至B点时速度大小
及此过程中轻杆对Q球所做的功W;
（2）Q球与轨道CD间的动摩擦因数
;
（3）Q球最终静止时与挡板间的距离
.
【答案】（1）
,
（2）
（3）
【解析】
(1)P球第一次运动至B点过程中，对PQ两球有:
所以:
P球第一次运动至B点过程中，轻杆对Q球所做的功
(2)Q球第一次运动至D点过程中，对PQ球有:
Q球与挡板碰撞后反向弹回，P球沿轨道AB上升的最大高度过程中，有:
联立可得μ=0.2
(3)Q球第一次运动至D点过程中，对PQ球有
每次碰撞后瞬间PQ两球的总动能均为碰撞前瞬间的
，对PQ球有:
解得:
练习册系列答案
阅读快车系列答案
相关题目
