题目内容
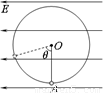
 用长为L的细线拉一质量为m的小球,小球带电量为+q,细线一端悬于固定点O,整个装置放在水平向右一足够大的匀强电场中,小球静止时细线与竖直方向的夹角为θ,电场范围足够大,不计空气阻力,重力加速度为g,求:
用长为L的细线拉一质量为m的小球,小球带电量为+q,细线一端悬于固定点O,整个装置放在水平向右一足够大的匀强电场中,小球静止时细线与竖直方向的夹角为θ,电场范围足够大,不计空气阻力,重力加速度为g,求:(1)匀强电场的电场强度大小;
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中的最大速度大小;
(3)在(2)问中,小球运动到最高点时细线对小球的拉力大小;
(4)若将小球拉至O点正下方最低点时给它一水平向右的初速度,小球在竖直面内做完整的圆周运动,这个初速度至少是多大?
分析:(1)小球静止A点时,受到重力、电场力和绳子的拉力而平衡,根据平衡条件求出电场强度的大小.
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中经过平衡位置时速度最大,根据动能定理求出最大速度.
(3)小球到最高点时,速度为零,向心力为零,绳子的拉力等于重力和电场力沿法线方向的合力.
(4)当小球恰好到达A点关于悬点的对称点时,由电场力和重力的合力提供向心力,根据牛顿第二定律求出小球经这点的速度,由动能定理求出初速度.
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中经过平衡位置时速度最大,根据动能定理求出最大速度.
(3)小球到最高点时,速度为零,向心力为零,绳子的拉力等于重力和电场力沿法线方向的合力.
(4)当小球恰好到达A点关于悬点的对称点时,由电场力和重力的合力提供向心力,根据牛顿第二定律求出小球经这点的速度,由动能定理求出初速度.
解答:解:(1)小球静止A点时,受力如图所示
据三力平衡条件,得
tanθ=
解得,E=
①
(2)小球运动到平衡位置时速度最大,由动能定理,得
qELsinθ-mgL(1-cosθ)=
mv2 ②
将①式代入,得
v=
③
小球从最底点到最高点时,速度为零,向心力为零,细线与竖直方向成α角,由动能定理,得
qELsinα-mgL(1-cosα)=0 ④
将①式代入④式,得
tanθsinα=1-cosα
解得,α=2θ
在最高点,重力与电场力合力的法线分力与拉力平衡,设线的拉力为F
F=mgcos2θ+qEsin2θ=mgcos2θ+mgtanθ?sin2θ=mg(2cos2θ-1)+mgtanθ?2sinθcosθ=mg
(3)设B点与A点对悬点O对称,即AB为圆轨迹的直径,当小球恰好能运动到B点时,就能在竖直面内恰好做完整的圆周运动
在B点,重力与电场力的合力提供向心力

=m
设将小球拉至O点正下方最低点时给它一水平向右的初速度为v0,由动能定理,得
-2mgLcosθ-qELsinθ=
mvB2-
mv02
解得
v0=
答:
(1)匀强电场的电场强度大小E=
;
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中的最大速度大小v=
;
(3)在(2)问中,小球运动到最高点时细线对小球的拉力大小为mg;
(4)若将小球拉至O点正下方最低点时给它一水平向右的初速度,小球在竖直面内做完整的圆周运动,这个初速度至少是v0=
.

据三力平衡条件,得
tanθ=
| qE |
| mg |
解得,E=
| mgtanθ |
| q |
(2)小球运动到平衡位置时速度最大,由动能定理,得
qELsinθ-mgL(1-cosθ)=
| 1 |
| 2 |
将①式代入,得
v=
|
小球从最底点到最高点时,速度为零,向心力为零,细线与竖直方向成α角,由动能定理,得
qELsinα-mgL(1-cosα)=0 ④
将①式代入④式,得
tanθsinα=1-cosα
解得,α=2θ
在最高点,重力与电场力合力的法线分力与拉力平衡,设线的拉力为F
F=mgcos2θ+qEsin2θ=mgcos2θ+mgtanθ?sin2θ=mg(2cos2θ-1)+mgtanθ?2sinθcosθ=mg
(3)设B点与A点对悬点O对称,即AB为圆轨迹的直径,当小球恰好能运动到B点时,就能在竖直面内恰好做完整的圆周运动
在B点,重力与电场力的合力提供向心力

| mg |
| cosθ |
| ||
| L |
设将小球拉至O点正下方最低点时给它一水平向右的初速度为v0,由动能定理,得
-2mgLcosθ-qELsinθ=
| 1 |
| 2 |
| 1 |
| 2 |
解得
v0=
2gLcosθ+
|
答:
(1)匀强电场的电场强度大小E=
| mgtanθ |
| q |
(2)将小球拉至O点正下方最低点由静止释放,小球向上摆动过程中的最大速度大小v=
|
(3)在(2)问中,小球运动到最高点时细线对小球的拉力大小为mg;
(4)若将小球拉至O点正下方最低点时给它一水平向右的初速度,小球在竖直面内做完整的圆周运动,这个初速度至少是v0=
2gLcosθ+
|
点评:本题小球的运动类似于单摆,关于平衡位置具有对称性,α=2θ.B点相当于竖直平面内圆周运动的最高点,也称为物理最高点.

练习册系列答案
相关题目
 (2013?深圳二模)如图所示,竖直平面内有一半 径R=0.9m、圆心角为60°的光滑圆弧 轨道PM,圆弧轨道最底端M处平滑 连接一长s=3m的粗糙平台MN,质 量分别为mA=4kg,mB=2kg的物块 A,B静置于M点,它们中间夹有长 度不计的轻质弹簧,弹簧与A连结,与B不相连,用细线拉紧A、B使弹簧处于压缩状态.N端有一小球C,用长为L的轻 绳悬吊,对N点刚好无压力.现烧断细线,A恰好能从P端滑出,B与C碰后总是交换速度.A、B、C均可视为质点,g取10m/s2,问:
(2013?深圳二模)如图所示,竖直平面内有一半 径R=0.9m、圆心角为60°的光滑圆弧 轨道PM,圆弧轨道最底端M处平滑 连接一长s=3m的粗糙平台MN,质 量分别为mA=4kg,mB=2kg的物块 A,B静置于M点,它们中间夹有长 度不计的轻质弹簧,弹簧与A连结,与B不相连,用细线拉紧A、B使弹簧处于压缩状态.N端有一小球C,用长为L的轻 绳悬吊,对N点刚好无压力.现烧断细线,A恰好能从P端滑出,B与C碰后总是交换速度.A、B、C均可视为质点,g取10m/s2,问: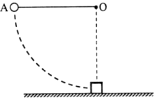 如图所示,质量为m的摆球用长为l的轻质细绳系于O点,O点正下方的粗糙水平地面上静止着一质量为M的钢块.现将摆球向左拉起,使细线水平,由静止释放摆球,摆球摆动至最低点时与钢块发生正碰,碰撞时间极短,碰后摆球反弹上升至最高点时与最低点的竖直高度差为
如图所示,质量为m的摆球用长为l的轻质细绳系于O点,O点正下方的粗糙水平地面上静止着一质量为M的钢块.现将摆球向左拉起,使细线水平,由静止释放摆球,摆球摆动至最低点时与钢块发生正碰,碰撞时间极短,碰后摆球反弹上升至最高点时与最低点的竖直高度差为