题目内容
光滑绝缘的水平面上,A和B两个带电小球相距2m,质量 .由静止释放的瞬间,A球的加速度为a;经时间t后,B球的加速度为2a,B球的速度为3m/s.
.由静止释放的瞬间,A球的加速度为a;经时间t后,B球的加速度为2a,B球的速度为3m/s. 求:(1)此时两球问的距离d.
(2)在时间t内,电势能的变化.

【答案】分析:(1)根据牛顿第二定律与库仑定律,即可求解;
(2)根据动量守恒定律,即可求出电势能的变化量.
解答:解:(1)设A、B两小球的电荷量分别为qA和qB释放两球的瞬间对小球A,
由库仑定律和牛顿第二定律得: ①
①
t秒末,选B球为研究对象,
由库仑定律和牛顿第二定律得: ②
②
由 ,
,
L=2m
由①、②两式解得:d=1m. ③
(2)设t秒末A、B小球的速度大小分别为vA和vB,对A、B两小球组成的系统,
由动量守恒得:
mAvA-mBvB=0 ④
解得vA=6m/s ⑤
两球的电势能减少, ⑥
⑥
则有,△EP=0.2J
答:(1)此时两球问的距离1m.
(2)在时间t内,电势能的变化0.2J.
点评:考查牛顿第二定律、库仑定律及动量守恒定律的应用与理解,注意动量守恒定律的矢量性,同时学会选择研究对象.
(2)根据动量守恒定律,即可求出电势能的变化量.
解答:解:(1)设A、B两小球的电荷量分别为qA和qB释放两球的瞬间对小球A,
由库仑定律和牛顿第二定律得:
 ①
①t秒末,选B球为研究对象,
由库仑定律和牛顿第二定律得:
 ②
②由
 ,
,L=2m
由①、②两式解得:d=1m. ③
(2)设t秒末A、B小球的速度大小分别为vA和vB,对A、B两小球组成的系统,
由动量守恒得:
mAvA-mBvB=0 ④
解得vA=6m/s ⑤
两球的电势能减少,
 ⑥
⑥则有,△EP=0.2J
答:(1)此时两球问的距离1m.
(2)在时间t内,电势能的变化0.2J.
点评:考查牛顿第二定律、库仑定律及动量守恒定律的应用与理解,注意动量守恒定律的矢量性,同时学会选择研究对象.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
 如图所示,在光滑绝缘的水平面上有两个相距无穷远的带电小球A、B,两球带同种电荷,A球质量为m以速度2v0向右运动,B球质量为4m以速度v0正对着A向左运动.设两球始终未相撞,求:
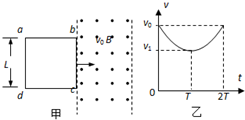
如图所示,在光滑绝缘的水平面上有两个相距无穷远的带电小球A、B,两球带同种电荷,A球质量为m以速度2v0向右运动,B球质量为4m以速度v0正对着A向左运动.设两球始终未相撞,求: 如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,
如图所示,在光滑绝缘的水平面上有一个用一根均匀导体围成的正方形线框abcd,其边长为L,总电阻为R,放在磁感应强度为B.方向竖直向下的匀强磁场的左边,图中虚线MN为磁场的左边界.线框在大小为F的恒力作用下向右运动,其中ab边保持与MN平行.当线框以速度v0进入磁场区域时,它恰好做匀速运动.在线框进入磁场的过程中,