题目内容
如图12所示,平行板电容器两极板间有场强为E的匀强电场,且带正电的极板接地.一质量为m、电荷量为+q的带电粒子(不计重力)从x轴上坐标为x0处静止释放.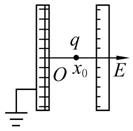
图12
(1)求该粒子在x0处的电势能![]() .
.
(2)试从牛顿第二定律出发,证明该带电粒子在极板间运动过程中,其动能与电势能之和保持不变.
解析:(1)W电=qEx0 ①
W电=-(![]() -0) ②
-0) ②
联立①②得:![]() =-qEx0 ③
=-qEx0 ③
(2)解法一:在带电粒子的运动方向上任取一点,设坐标为x.
由牛顿第二定律可得qE=ma ④
由运动学公式得v2x=2a(x-x0) ⑤
联立④⑤式求得Ekx=![]() mv2x=qE(x-x0) ⑥
mv2x=qE(x-x0) ⑥
Ex=Ekx+EPx=qE(x-x0)+(-qEx)=-qEx0=EPx0. ⑦
解法二:在x轴上任取两点x1、x2,速度分别为v1、v2.
F=qE=ma
v22-v21=2a(x2-x1)
联立得![]() mv22-
mv22-![]() mv21=qE(x2-x1)
mv21=qE(x2-x1)
所以![]() mv22+(-qEx2)=
mv22+(-qEx2)=![]() mv21+(-qEx1)
mv21+(-qEx1)
即![]()
故在其运动过程中,其动能和势能之和保持不变.
答案:(1)-qEx0 (2)见解析

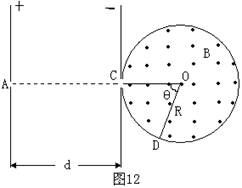 (06年广东卷)(17 分)在光滑绝缘的水平桌面上,有两个质量均为m,电量为+q的完全相同的带电粒子P1和P2,在小孔A处以初速度为零先后释放。在平行板间距为d的匀强电场中加速后,P1从C处对着圆心进入半径为R的固定圆筒中(筒壁上的小孔C只能容一个粒子通过),圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场。P1每次与筒壁发生碰撞均无电荷迁移,P1进入磁场第一次与筒壁碰撞点为D,∠COD=θ,如图12所示。延后释放的P2,将第一次欲逃逸出圆筒的P1正碰圆筒内,此次碰撞刚结束,立即改变平行板间的电压,并利用P2与P1之后的碰撞,将P1限制在圆筒内运动。碰撞过程均无机械能损失。设d=
(06年广东卷)(17 分)在光滑绝缘的水平桌面上,有两个质量均为m,电量为+q的完全相同的带电粒子P1和P2,在小孔A处以初速度为零先后释放。在平行板间距为d的匀强电场中加速后,P1从C处对着圆心进入半径为R的固定圆筒中(筒壁上的小孔C只能容一个粒子通过),圆筒内有垂直水平面向上的磁感应强度为B的匀强磁场。P1每次与筒壁发生碰撞均无电荷迁移,P1进入磁场第一次与筒壁碰撞点为D,∠COD=θ,如图12所示。延后释放的P2,将第一次欲逃逸出圆筒的P1正碰圆筒内,此次碰撞刚结束,立即改变平行板间的电压,并利用P2与P1之后的碰撞,将P1限制在圆筒内运动。碰撞过程均无机械能损失。设d=![]() ,求:在P2和P1相邻两次碰撞时间间隔内,粒子P1与筒壁的可能碰撞次数。
,求:在P2和P1相邻两次碰撞时间间隔内,粒子P1与筒壁的可能碰撞次数。
附:部分三角函数值
|
|
|
|
|
|
|
|
|
|
tan | 3.08 | 1.37 | 1.00 | 0.73 | 0.58 | 0.48 | 0.41 | 0.36 | 0.32 |