题目内容
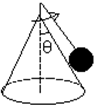如图所示，在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球，圆锥顶角为2θ，若要小球离开锥面，则小球的角速度至少为多少？（重力加速度为g）分析：小球刚要离开锥面时，支持力为零，分析小球的受力情况，由合力提供向心力，根据牛顿第二定律列式求出该临界角速度ω0．
解答：解：小球刚要离开锥面时，支持力为零，小球受到重力mg、绳的拉力T，设此时角速度为ω0，
根据牛顿第二定律得：
Tsinθ=mω02Lsinθ ①
Tcosθ=mg； ②
由①②两式得：
mgtanθ=mω02Lsinθ
解得：ω0=
答：若要小球离开锥面，则小球的角速度至少为
．
根据牛顿第二定律得：
Tsinθ=mω02Lsinθ ①
Tcosθ=mg； ②
由①②两式得：
mgtanθ=mω02Lsinθ
解得：ω0=
|
答：若要小球离开锥面，则小球的角速度至少为
|
点评：本题的关键点在于分析小球向心力的来源，抓住小球刚离开圆锥体表面时支持力为零，直接应用向心力公式求解．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内作半径不同的匀速圆周运动，其中球P的轨道半径较大，则可判定（ ）
如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则（ ） 如图所示，在光滑的圆锥面内，两个质量不相同的小球P和Q，沿其内表面在不同的水平面内做半径不同的匀速圆周运动，其中球P的轨道半径较大，则 
| A．球P的角速度较小 | B．球P的向心力较小 |
| C．球P的加速度较大 | D．球P的线速度较大 |
