题目内容
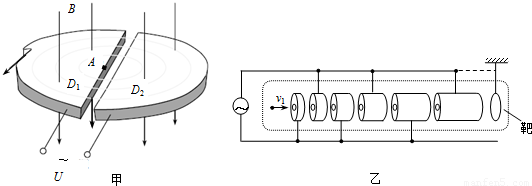
N个长度逐个增大的金属筒和一个靶沿轴线排列成一串,如图所示(图中只画出4个圆筒,作为示意),各筒和靶相间地连接到频率为f,最大电压值为U的正弦交流电源的两端,整个装置放在高度真空容器中,圆筒的两底面中心开有小孔,现有一电量为q、质量为m的正离子沿轴线射入圆筒,并将在圆筒间及圆筒与靶间的缝隙处受到电场力作用而加速(设圆筒内部没有电场),缝隙的宽度很小,离子穿过缝隙的时间可以不计,已知离子进入第一个圆筒左端的速度为v1,且此时第一、二两个圆筒间的电势差U1-U2=-U,为使打到靶上的离子获得最大能量,各个圆筒的长度应满足什么条件?并求出在这种情况下打到靶上的离子能量.

答案:
解析:
解析:
解析:正离子每次经过缝隙时都能得到加速必须满足在筒中飞行时间![]()
所以第一个筒长度![]()
进入第二个筒时速度为v2,则![]() ①
①
第二个筒长![]()
进入第三个筒的速度为v3,则![]() ②
②
第三个筒长![]()
进入第n个筒的速度vn满足![]() ③
③
第n个筒的长度为![]() ,解以上各式得:
,解以上各式得:
![]()
![]()
由动能定理得:![]()
![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目