题目内容
如图所示，两根长度不同的细绳，一端固定于O点，另一端各系一个完全相同的小铁球，两小球恰好在同一水平面内做匀速圆周运动，，AOC=45°，∠BOC=30°，则两球运动的半径之比rA：rB= ；两绳中张力之比FA：FB= ；两球运动的周期之比TA：TB= ．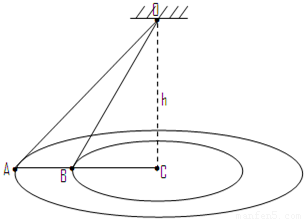
【答案】分析：AB两球都在水平面内做匀速圆周运动，A球运动的半径等于AC，B球运动的半径等于BC．两球均由重力和细绳拉力的合力提供向心力，根据牛顿第二定律求出绳中张力和周期，再求解它们的比值．
解答：解：两球运动的半径之比rA：rB=htan45°：htan30°=3：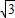
两绳中张力之比FA：FB=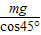
：
=
：
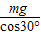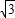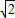
设细绳与竖直方向的夹角为α
由牛顿第二定律得
mgtanα=m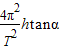
得到T=2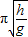
所以两球运动的周期之比TA：TB=1：1．
故答案为：3：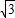
，
：
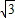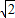，1：1．
点评：本题是圆锥摆问题，分析受力，确定向心力是关键．对于圆锥摆的周期与单摆的周期类似，可类比记忆．
解答：解：两球运动的半径之比rA：rB=htan45°：htan30°=3：
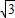
两绳中张力之比FA：FB=
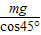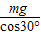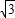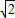
：=：设细绳与竖直方向的夹角为α
由牛顿第二定律得
mgtanα=m
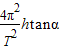
得到T=2
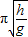
所以两球运动的周期之比TA：TB=1：1．
故答案为：3：
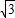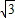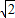，：，1：1．点评：本题是圆锥摆问题，分析受力，确定向心力是关键．对于圆锥摆的周期与单摆的周期类似，可类比记忆．
练习册系列答案
相关题目
