题目内容
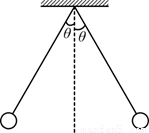
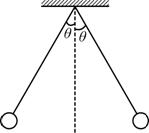
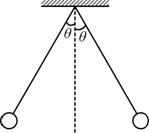
 用两根长度均为L的绝缘细线各系一个小球,并悬挂于同一点.已知两小球质量均为m,当它们带上等量同种电荷时,两细线与竖直方向的夹角均为θ,如图所示.若已知静电力常量为k,重力加速度为g.求:
用两根长度均为L的绝缘细线各系一个小球,并悬挂于同一点.已知两小球质量均为m,当它们带上等量同种电荷时,两细线与竖直方向的夹角均为θ,如图所示.若已知静电力常量为k,重力加速度为g.求:(1)小球所受拉力的大小;
(2)小球所带的电荷量.
分析:对其中一个小球受力分析,由共点力的平衡条件可得出小球所受拉力的大小和小球受到的库仑力,由库仑力公式可得出小球所带电荷量.
解答: 解:(1)对小球进行受力分析,如图所示.
解:(1)对小球进行受力分析,如图所示.
设绳子对小球的拉力为T,
根据平衡条件得:
=cosθ,
T=
(2)设小球在水平方向受到库仑力的大小为F,
=tanθ
F=mgtanθ
根据库仑定律得:
答:(1)小球所受拉力的大小是
;
(2)小球所带的电荷量是
.
 解:(1)对小球进行受力分析,如图所示.
解:(1)对小球进行受力分析,如图所示.设绳子对小球的拉力为T,
根据平衡条件得:
| mg |
| T |
T=
| mg |
| cosθ |
(2)设小球在水平方向受到库仑力的大小为F,
| F |
| mg |
F=mgtanθ
根据库仑定律得:
|
|
|
答:(1)小球所受拉力的大小是
| mg |
| cosθ |
(2)小球所带的电荷量是
|
点评:本题两边的球是对称的,故分析其中一个小球即可得出正确结论;
在电场中处理问题的方法与力学是一致的,做好受力分析是解决问题的关键.
在电场中处理问题的方法与力学是一致的,做好受力分析是解决问题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目