题目内容

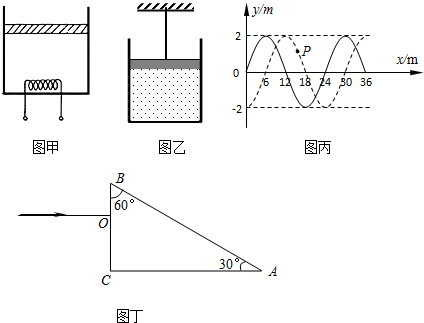
如右图所示，将一根光滑的细金属棒折成“V”形，顶角为2θ，其对称轴竖直，在其中一边套上一个质量为m的小金属环P.

(1)若固定“V”形细金属棒，小金属环P从距离顶点O为x的A点处由静止自由滑下，则小金属环由静止下滑至顶点O需多长时间？

(2)若小金属环P随“V”形细金属棒绕其对称轴以每秒n转匀速转动时，则小金属环离对称轴的距离为多少？

解析：　(1)设小金属环沿棒运动的加速度为a，滑至O点用时为t，由牛顿第二定律得mgcos θ＝ma

由运动学公式得x＝at2

联立解得t＝.

(2)设小金属环离对称轴的距离为r，由牛顿第二定律和向心力公式得

mgcot θ＝mrω2，ω＝2πn

联立解得r＝

答案：　(1) 　(2)     

练习册系列答案
相关题目
（1）在光电效应的实验中，某同学用同一光电管在不同实验条件下得到了三条光电流与电压的关系曲线，如图所示．下列判断正确的是
BCE
BCE
．
A．甲光的频率大于乙光的频率
B．乙光的波长大于丙光的波长
C．若更换不同的光电管，对应的截止频率也将不同
D．甲光对应的光电子最大初动能大于丙光的光电子最大初动能
E．甲光的光强大于乙光的光强
（2）在足够长的光滑固定水平杆上，套有一个质量为m=0.5kg的光滑圆环．一根长尾L=1m的轻绳，一端拴在环上，另一端系着一个质量为M=2kg的木块，如图所示．现有一质量为m0=20g的子弹以v0=1000m/s的水平速度射入木块，子弹穿出木块时的速度为u=200m/s，子弹与木块作用的时间极短，取g=10m/s2．求
①当子弹射穿木块时，轻绳的拉力大小F；
②当子弹射穿木块后，木块向右摆动的最大高度h．
（2011?江苏模拟）[选做题]本题包括A、B、C三小题，请选定其中两题，并在相应的答题区域内作答．若三题都做，则按A、B两题评分．
A．（选修模块3-3）
（1）由以下数据能估算出水分子直径的是
D
D

A．水的质量、水的体积和阿伏加德罗常数
B．水的质量、水的密度和阿伏加德罗常数
C．水的摩尔质量和阿伏加德罗常数
D．水的摩尔体积和阿伏加德罗常数
（2）如图乙所示，用一根与绝热活塞相连的细线将绝热气缸悬挂在某一高度静止不动，气缸开口向上，内封闭一定质量的气体（分子间的相互作用力忽略不计），缸内活塞可以无摩擦移动且不漏气，现将细线剪断，让气缸自由下落，下列说法正确的是
BD
BD

A．气体压强减小，气体对外界做功
B．气体压强增大，外界对气体做功
C．气体体积增大，气体内能减小
D．气体体积减小，气体内能增大
（3）如图甲所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体．活塞的质量为m，横截面积为S，此时活塞处于平衡状态，气体的温度为T1．现通过电热丝缓慢加热气体，在气体吸收热量为Q的过程中，气体对活塞做功的大小为W．已知大气压强为p0，重力加速度为g，不计活塞与气缸的摩擦．求：
①气体的压强；
②加热过程中气体的内能增加量；
B．（选修模块3-4）
（1）下列说法中正确的是
AC
AC
．
A．激光比普通光源的相干性好
B．紫外线在水中的传播速度大于红外线在水中的传播速度
C．在光的衍射实验中，出现明条纹的地方光子到达的概率较大
D．接收电磁波时首先要进行调频
（2）一列沿x轴正方向传播的简谐横波，t=0时刻的波形如图中实线所示，t=0.2s时刻的波形如图丙中虚线所示，则：
A．质点P的运动方向向右
B．波的周期可能为0.27s
C．波的传播速度可能为630m/s
D．波的频率可能为1.25Hz
（3）如图丁所示，ABC为玻璃三棱镜的横截面，∠A=30°，∠B=60°，BC=3cm，一条平行于AC边的光线从O点垂直射向棱镜，OC=2cm，已知棱镜对光的折射率为n=1.5，试求光线在棱镜内传播的最短时间是多少？
C． （选修模块3-5）
（1）正电子（PET）发射计算机断层显像的基本原理是：将放射性同位素
 
15
8
O注入人体，参与人体的代谢过程．
 
15
8
O在人体内衰变放出正电子，与人体内负电子相遇而湮灭转化为一对光子，被探测器探测到，经计算机处理后产生清晰的图象．根据PET原理，回答下列问题：
①写出
 
15
8
O的衰变的方程式
 
15
8
O→
 
15
7
N+
 
0
1
e
 
15
8
O→
 
15
7
N+
 
0
1
e
．
②将放射性同位素
 
15
8
O注入人体，
 
15
8
O的主要用途
B
B

A．利用它的射线       B．作为示踪原子
C．参与人体的代谢过程  D．有氧呼吸
③PET中所选的放射性同位素的半衰期应
短
短
．（填“长”或“短”或“长短均可”）
（2）一辆小车在光滑水平面上以v1=1m/s的速度向右运动，小车的质量为M=100kg，一质量为m=50kg的人从小车的右端迎面跳上小车，接触小车前的瞬间人的水平速度大小为v2=5.6m/s．求人跳上小车后，人和小车的共同速度和人跳上小车的过程中人对小车做的功．
[选做题]本题包括A、B、C三小题，请选定其中两题，并在相应的答题区域内作答．若三题都做，则按A、B两题评分．
A．（选修模块3-3）
（1）由以下数据能估算出水分子直径的是______
A．水的质量、水的体积和阿伏加德罗常数
B．水的质量、水的密度和阿伏加德罗常数
C．水的摩尔质量和阿伏加德罗常数
精英家教网

D．水的摩尔体积和阿伏加德罗常数
（2）如图乙所示，用一根与绝热活塞相连的细线将绝热气缸悬挂在某一高度静止不动，气缸开口向上，内封闭一定质量的气体（分子间的相互作用力忽略不计），缸内活塞可以无摩擦移动且不漏气，现将细线剪断，让气缸自由下落，下列说法正确的是______
A．气体压强减小，气体对外界做功
B．气体压强增大，外界对气体做功
C．气体体积增大，气体内能减小
D．气体体积减小，气体内能增大
（3）如图甲所示，一圆柱形绝热气缸竖直放置，通过绝热活塞封闭着一定质量的理想气体．活塞的质量为m，横截面积为S，此时活塞处于平衡状态，气体的温度为T1．现通过电热丝缓慢加热气体，在气体吸收热量为Q的过程中，气体对活塞做功的大小为W．已知大气压强为p0，重力加速度为g，不计活塞与气缸的摩擦．求：
①气体的压强；
②加热过程中气体的内能增加量；
B．（选修模块3-4）
（1）下列说法中正确的是______．
A．激光比普通光源的相干性好
B．紫外线在水中的传播速度大于红外线在水中的传播速度
C．在光的衍射实验中，出现明条纹的地方光子到达的概率较大
D．接收电磁波时首先要进行调频
（2）一列沿x轴正方向传播的简谐横波，t=0时刻的波形如图中实线所示，t=0.2s时刻的波形如图丙中虚线所示，则：
A．质点P的运动方向向右
B．波的周期可能为0.27s
C．波的传播速度可能为630m/s
D．波的频率可能为1.25Hz
（3）如图丁所示，ABC为玻璃三棱镜的横截面，∠A=30°，∠B=60°，BC=3cm，一条平行于AC边的光线从O点垂直射向棱镜，OC=2cm，已知棱镜对光的折射率为n=1.5，试求光线在棱镜内传播的最短时间是多少？
C． （选修模块3-5）
（1）正电子（PET）发射计算机断层显像的基本原理是：将放射性同位素
 158
O注入人体，参与人体的代谢过程．
 158
O在人体内衰变放出正电子，与人体内负电子相遇而湮灭转化为一对光子，被探测器探测到，经计算机处理后产生清晰的图象．根据PET原理，回答下列问题：
①写出
 158
O的衰变的方程式______．
②将放射性同位素
 158
O注入人体，
 158
O的主要用途______
A．利用它的射线       B．作为示踪原子
C．参与人体的代谢过程  D．有氧呼吸
③PET中所选的放射性同位素的半衰期应______．（填“长”或“短”或“长短均可”）
（2）一辆小车在光滑水平面上以v1=1m/s的速度向右运动，小车的质量为M=100kg，一质量为m=50kg的人从小车的右端迎面跳上小车，接触小车前的瞬间人的水平速度大小为v2=5.6m/s．求人跳上小车后，人和小车的共同速度和人跳上小车的过程中人对小车做的功．
光纤通信是一种现代化的通讯手段，它可以提供大容量，高速度、高质量的通信服务。为了研究问题的方便，我们将光导纤维简化为一根长直的玻璃管，如右图所示，设此玻璃管长为L，折射率为n，且光在玻璃的内界面上恰好发生全反射。已知光在真空中的传播速度为c，则光通过此段玻璃管所需的时间为

A.nL/c             B.n2L/c               C.nL/c2                 D.n2L/c2

（1）在光电效应的实验中，某同学用同一光电管在不同实验条件下得到了三条光电流与电压的关系曲线，如图所示．下列判断正确的是______．
A．甲光的频率大于乙光的频率
B．乙光的波长大于丙光的波长
C．若更换不同的光电管，对应的截止频率也将不同
D．甲光对应的光电子最大初动能大于丙光的光电子最大初动能
E．甲光的光强大于乙光的光强
（2）在足够长的光滑固定水平杆上，套有一个质量为m=0.5kg的光滑圆环．一根长尾L=1m的轻绳，一端拴在环上，另一端系着一个质量为M=2kg的木块，如图所示．现有一质量为m=20g的子弹以v=1000m/s的水平速度射入木块，子弹穿出木块时的速度为u=200m/s，子弹与木块作用的时间极短，取g=10m/s2．求
①当子弹射穿木块时，轻绳的拉力大小F；
②当子弹射穿木块后，木块向右摆动的最大高度h．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网