题目内容
伞边缘半径为r,且高出地面为h,若使雨伞以角速度ω旋转,求雨滴自伞边缘甩出后落于地面形成的大圆圈半径R.
分析:根据v=ωr求出雨滴离开伞时的初速度,根据平抛运动求出求出雨滴的水平位移,结合几何关系求出雨滴自伞边缘甩出后落于地面形成的大圆圈半径R.
解答:解:雨滴运动的俯视图如图,由图可知:
s=vt
h=
gt2
v=ωr
联合解得:s=
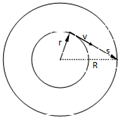
由几何关系得:R=
=r
.
答:雨滴自伞边缘甩出后落于地面形成的大圆圈半径为r
.
s=vt
h=
| 1 |
| 2 |
v=ωr
联合解得:s=
|

由几何关系得:R=
| s2+r2 |
1+
|
答:雨滴自伞边缘甩出后落于地面形成的大圆圈半径为r
1+
|
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,灵活运用运动学公式进行求解.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目