题目内容
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10 m/s2.试求: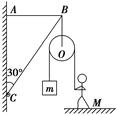
(1)此时人对地面的压力的大小;
(2)轻杆BC和绳AB所受力的大小.
(1) 200N 方向竖直向上(2) 400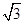 N 200
N 200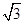 N
N
解析试题分析:(1)因匀速提起重物,则FT=mg,且绳对人的拉力为mg,
所以地面对人的支持力为:FN=Mg-mg=(50-30)×10 N=200 N,
又牛顿第三定律知,人对地面的压力也为200N 方向竖直向上。
(2)定滑轮对B点的拉力方向竖直向下,大小为2mg,杆对B点的弹力方向沿杆的方向,如图所示,由共点力平衡条件得:
FAB=2mgtan 30°=2×30×10×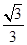 N
N
=200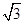 N
N
FBC=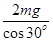 =
= N=400
N=400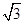 N
N
考点:考查了力的平衡条件的应用
点评:本题通过数学三角函数解题,充分体现学科间的整合.

练习册系列答案
相关题目
 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求: 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB连接使杆与竖直墙壁保持30°的夹角.若在B点通过BO绳悬挂一个定滑轮(不计滑轮重力及摩擦),某人用跨在滑轮上的细绳匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过水平细绳AB连接使杆与竖直墙壁保持30°的夹角.若在B点通过BO绳悬挂一个定滑轮(不计滑轮重力及摩擦),某人用跨在滑轮上的细绳匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg,g取10m/s2.试求: 如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过细绳AB使杆水平、细线与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg.试求:
如图所示,轻杆BC的C点用光滑铰链与墙壁固定,杆的B点通过细绳AB使杆水平、细线与竖直墙壁保持30°的夹角.若在B点悬挂一个定滑轮(不计重力),某人用它匀速地提起重物.已知重物的质量m=30kg,人的质量M=50kg.试求: 如图所示,轻杆BC的一端铰接于C,另一端悬挂重物G,并用细绳绕过定滑轮用力拉住.开始时,∠BCA>90°,现用拉力F使∠BCA缓慢减小,直到BC接近竖直位置的过程中,杆BC所受的压力( )
如图所示,轻杆BC的一端铰接于C,另一端悬挂重物G,并用细绳绕过定滑轮用力拉住.开始时,∠BCA>90°,现用拉力F使∠BCA缓慢减小,直到BC接近竖直位置的过程中,杆BC所受的压力( ) 如图所示,轻杆BC的一端铰接于C,另一端挂重物G,并用细绳绕过定滑轮拉住.开始时BC向下倾斜,现用力F拉绳,使BC缓慢接近竖直位置,在此过程中BC受到的圧力( )
如图所示,轻杆BC的一端铰接于C,另一端挂重物G,并用细绳绕过定滑轮拉住.开始时BC向下倾斜,现用力F拉绳,使BC缓慢接近竖直位置,在此过程中BC受到的圧力( )