题目内容
在光滑平面中，有一转动轴垂直于此平面，交点O的上方h处固定一细绳的一端，绳的另一端固定一质量为m的小球B，绳长AB=l＞h，小球可随转动轴转动并在光滑水平面上做匀速圆周运动，如图所示，问要使球不离开水平面，转动轴转速的最大值是多少？
如图所示，以小球为研究对象，小球受三个力的作用，重力mg、水平面支持力N、绳子拉力F．
在竖直方向合力为零，在水平方向所需向心力为
，而R=htanθ，得
Fcosθ+N=mg
Fsinθ=
=mω2R=m4π2n2R=m4π2n2htanθ
当球即将离开水平面时，N=0，转速n有最大值．
N=mg-m4π2n2tanθ=0
n=
．
答：要使球不离开水平面，转动轴转速的最大值是
．
在竖直方向合力为零，在水平方向所需向心力为
| mv2 |
| R |
Fcosθ+N=mg
Fsinθ=
| mv2 |
| R |
当球即将离开水平面时，N=0，转速n有最大值．
N=mg-m4π2n2tanθ=0
n=
| 1 |
| 2π |
|
答：要使球不离开水平面，转动轴转速的最大值是
| 1 |
| 2π |
|
练习册系列答案
阅读快车系列答案
相关题目
（2010?上海模拟）一块木板可绕过O点的光滑水平轴在竖直平面内转动，木板上放有一木块，木板右端受到竖直向上的作用力F，从图中位置A缓慢转到位置B，木块相对木板不发生滑动．则在此过程中，力F和F的力矩MF大小的变化情况是（ ）
（1）如图所示，某种变速自行车有三个链轮和六个飞轮，链轮和飞轮的齿数如下表所示．该自行车的前后轮周长为2m，人脚踩踏板的转速为每秒钟1.5转．若采用的链轮和飞轮齿数分别为48和24，则该种组合下自行车行驶时的速度为
（2011?静安区一模）一块木板可绕过O点的光滑水平轴在竖直平面内转动，木板上放有一木块，木板右端受到始终与木板垂直的力F，从图中位置A缓慢转到位置B，木块相对木板不发生滑动．则在此过程中，力F和F的力矩MF大小的变化情况是（ ）
一块木板可绕过O点的光滑水平轴在竖直平面内转动，木板上放有一物块，木板右端受到竖直向上的作用力F，从图中位置A缓慢转到位置B，物块相对木板不发生滑动．则在此过程中，关于物块受到的摩擦力f的说法正确的是（ ）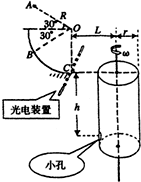
如图所示，半径R=0.80m的