题目内容
在光滑水平桌面上,有一长为l=
图
(1)当两滑块都与挡板相撞后,板C的速度多大?
(2)到两个滑块都与挡板碰撞为止,板的位移大小和方向如何?
解析:由于爆炸A、B相互作用系统满足动量守恒,A、B分离后以不同速率奔向挡板,A先到达挡板与C作用,发生完全非弹性碰撞,以后C与B有相对运动,直到碰撞为止,整个过程满足动量守恒.
(1)设向左的方向为正方向,对A、B组成的系统由动量守恒定律有:
mAvA+mBvB=0得vB=
对A、B、C组成的系统开始时静止由动量守恒有(mA+mB+mC)vC=0得vC=0,即最终木板C的速度为0.
(2)A先与C相碰由动量守恒:mAvA=(mA+mC)v共,所以v共=
从炸药爆炸到A、C相碰的时间:t1= s,此时B距C的右壁sB=
s,此时B距C的右壁sB=![]() -vBt1=
-vBt1=
t2=![]() =0.3 s,故C向左的位移
=0.3 s,故C向左的位移
Δsc=v共t=1×
答案:(1)0 (2)

练习册系列答案
相关题目
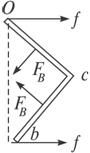
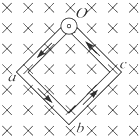 如图所示,在光滑水平桌面上,有两根弯成直角的相同金属棒,它们的一端均可绕固定转动轴O自由转动,另一端b互相接触,组成一个正方形线框.正方形每边长度均为L,匀强磁场的方向垂直桌面向下,当线框中通以图示方向的电流I时,两金属棒在b点的相互作用力为f,则此时磁感应强度的大小为
如图所示,在光滑水平桌面上,有两根弯成直角的相同金属棒,它们的一端均可绕固定转动轴O自由转动,另一端b互相接触,组成一个正方形线框.正方形每边长度均为L,匀强磁场的方向垂直桌面向下,当线框中通以图示方向的电流I时,两金属棒在b点的相互作用力为f,则此时磁感应强度的大小为